Giải Toán 11 Kết nối tri thức: Bài 1: Giá trị lượng giác của góc lượng giác

Hướng dẫn Giải Toán 11 Kết nối tri thức Bài 1: Giá trị lượng giác của góc lượng giác ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 11 trang 6

Hoạt động 1: Nhận biết khái niệm góc lượng giác

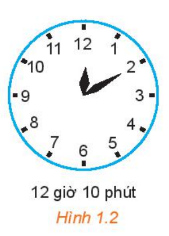
Trên đồng hồ ở Hình 1.2, kim phút đang chỉ đúng số 2.

a) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay ngược chiều kim đồng hồ để nó chỉ đúng số 12?

b) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay của kim đồng hồ để nó chỉ đúng số 12?

c) Có bao nhiêu cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12?

Lời giải :

a) Khi kim phút quay theo ngược chiều kim đồng hồ để nó chỉ đúng số 12, kim phút quay 2/12=1/6

 phần của vòng tròn

b) Khi kim phút quay theo đúng chiều kim đồng hồ để nó chỉ đúng số 12, kim phút quay 10/12=5/6

phần của vòng tròn

c) Có 2 cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12, đó

là ngược chiều kim đồng hồ và cùng chiều kim đồng hồ

Giải Toán 11 trang 7

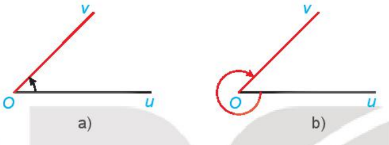
Luyện tập 1:Cho góc hình học uOv = 45^∘ Xác định số đo của góc lượng giác (Ou,Ov) trong mỗi trường hợp sau

Lời giải:

Ta có:

a)  Góc lượng giác tia đầu Ou, tia cuối Ov, quay theo chiều dương có số đo là

sđ(Ou, Ov) = 45°+ k.360^∘

b)  Góc lượng giác có tia đầu Ou, tia cuối Ov, quay theo chiều âm có số đo là

sđ(Ou, Ov) = – (360° – 45°) = – 315°+ k.360^∘

Hoạt động 2: Nhận biệt hệ thức Chasles

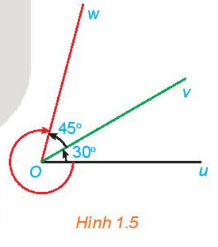
Cho ba tia Ou, Ov, Ow với số đo của các góc hình học uOv và vOw lần lượt là 30^∘ và 45^∘
a) Xác định số đo của ba góc lượng giác (Ou, Ov), (Ov, Ow) và (Ou, Ow) được chỉ ra ở Hình 1.5

b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để sđ(Ou,Ov) + sđ(Ov,Ow) = sđ(Ou,Ow) + k360^∘

Lời giải:

a) Số đo của ba góc lượng giác

sđ(Ou,Ov) = 30^∘+n.360^∘

sđ(Ov,Ow) = 45^∘+m.360^∘

sđ(Ou,Ow) = 75^∘+k.360^∘

b) Với các góc lượng giác ở câu a) ta có:

sđ(Ou,Ov)+sđ(Ov,Ow)=30^∘+n.360^∘+45^∘+m.360^∘

=75^∘+(n+m).360^∘

=75^∘+k.360^∘=sđ(Ou,Ow)

với k = n + m

Giải Toán 11 trang 8

Luyện tập 2:  Cho một góc lượng giác (Ox,Ou) có số đo 240^∘ và một góc lượng giác (Ox,Ov) có số đo −270^∘. Tính số đo của các góc lượng giác (Ou,Ov).

Lời giải:

Số đo của các góc lượng giác tia đầu Ou, tia cuối Ov :

sđ(Ou,Ov)=sđ(Ox,Ov)−sđ(Ox,Ou)+k360∘(k∈Z)

= −270^∘−240^∘+k.360^∘=−510^∘+k.360^∘

=−150^∘+(k−1)360^∘=−150^∘+n.360^∘      (n=k−1,n∈Z)

Vậy các góc lượng giác (Ou,Ov)có số đo là −150^∘+n.360^∘(n∈Z).

Giải Toán 11 trang 9

Luyện tập 3:

a) Đổi từ độ sang radian các số đo sau: 360^∘;−450^∘

b) Đổi từ radian sang độ các số đo sau: 3π;−11π/5

Lời giải:

a)Ta có:

 360^∘ = 360 × π/180 = π/2
−450^∘ = −450 × π/180 = −π/4
b) Ta có: 

3π = 3π × (180/π)^∘= 540^∘
−11π/5 = −11π/5 × (180/π)^∘= −396^∘

Hoạt động 3: Xây dựng công thức tính độ dài của cung tròn

Cho đường tròn bán kính R.

a) Độ dài của cung tròn có số đo bằng 1 rad là bao nhiêu

b) Tính độ dài l của cung tròn có số đo α rad.

Lời giải:

    a) Độ dài của cung tròn có số đo bằng 1 rad là bằng bán kính R.

    b) Độ dài l của cung tròn có số đo α rad: l = Rα.

Giải Toán 11 trang 10

Hoạt động 4: Nhận biết khái niệm đường tròn lượng giác

Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính R = 1. Chọn điểm gốc của đường tròn là giao điểm A(1;0) của đường tròn với trục Ox. Ta quy ước chiều dương của đường tròn là chiều ngược chiều quy kim đồng hồ và chiều âm là chiều quay của kim đồng hồ

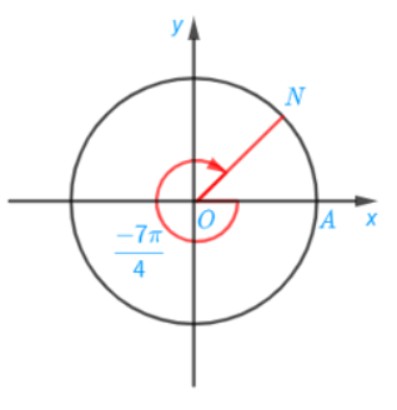
a) Xác định điểm M trên đường tròn sao cho sđ(OA,OM) = 5π/4

b) Xác định điểm N trên đường tròn sao cho sđ(OA,ON) = −7π/4

Lời giải:

a) sđ(OA,OM) = 5π/4 = π + π/4

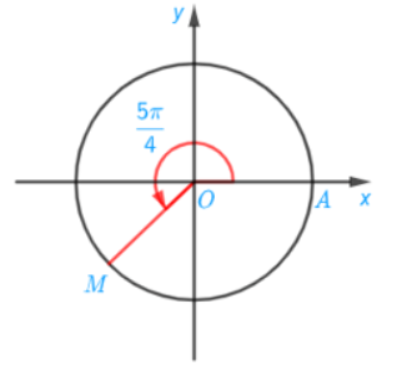
b) sđ(OA,ON) = −7π/4 = −(3π/4 + π)

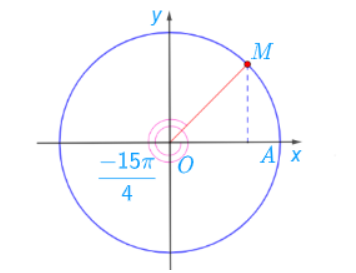
Luyện tập 4: Xác định điểm M và N trên đường tròn lượng giác lần lượt biểu diễn các góc lượng giác có số đo bằng −15π/4 và 420^∘

Lời giải:

Điểm biểu diễn góc lượng giác có số đo bằng −15π/4 = −7π/4 + (−1).2π được xác định là điểm M.

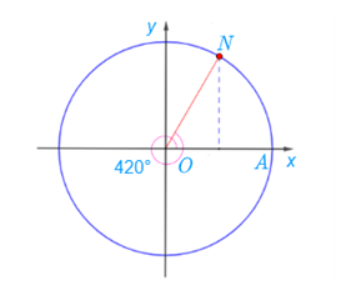
Ta có : 420/360 = 1+1/6

Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo 420^∘

Giải Toán 11 trang 11

Hoạt động 5: Nhắc lại giá trị lượng giác sinα,cosα,tanα,cotα của góc α(0^∘≤α≤180^∘) đã học ở lớp 10 (H.1.)

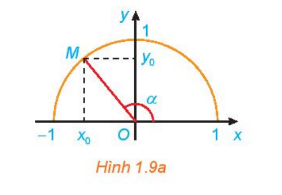
Lời giải:

sinα = y₀

cosα = x₀

tanα = y₀ / x₀ = sinx / cosx  nếu x₀ ≠ 0

cotα = x₀ / y₀ = cosx / sinx nếu y₀ ≠ 0

Giải Toán 11 trang 12

Luyện tập 5: Cho góc lượng giác có số đo bằng 5π/6

a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.

b) Tính các giá trị lượng giác của góc lượng giác đã cho.

Lời giải:

a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo 5π6

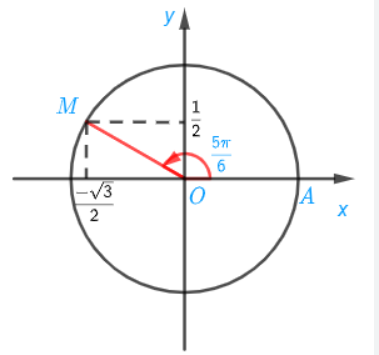
b) Ta có:

sin (5π/6) = 1/2;

cos (5π/6) = −√3/2;

tan (5π6) = −√3/3;

cot (5π6) = −√3;

Giải Toán 11 trang 13

Luyện tập 6: Sử dụng máy tính cầm tay để:

a) Tính: cos 3π/7; tan (−37∘25′)

b) Đổi 179^∘23′30′′ sang radian

c) Đổi 79 (rad) sang độ

Lời giải:

Sử dụng máy tính cầm tay

a)

cos 3π/7 ≈  0.2225;

tan (−37^∘25′) ≈  −0.765;

b)  179°23'30" ≈ 3,130975234 (rad).

c) 7/9 rad ≈ 44^∘33′48.18′′

Hoạt động 6: Nhận biết các công thức lượng giác cơ bản

a) Dựa vào định nghĩa của sin α và cos α, hãy tính sin²α + cos²α

b) Sử dụng kết quả của HĐ5a và định nghĩa của tan α, hãy tính 1 + tan²α

Lời giải:

a) sin²α + cos²α = x² + y² = OM² = 1 (Áp dụng định lí Pytagore trong tam giác vuông)

b) 1 + y²/x² = x² + y²/x² = 1/cos²α

Giải Toán 11 trang 14

Luyện tập 7: Tính các giá trị lượng giác của góc α, biết cosα = −2/3 và π < α < 3π/2

Lời giải:

Vì π < α < 3π/2 nên sin α > 0 

Mặt khác, từ sin 2α + cos 2α = 1 suy ra sin α = √1−cos 2α = √1−4/9 = √5/3

Do đó :  tan α  = sin α / cos α 

                         = √5/3 /2/3

                          =−√5/2;

               cot α = 1/tan α = −2√5

Hoạt động 7: Nhận biết liên hệ giữa giá trị lượng giác của các góc đối nhau

Xét hai điểm M. N trên đường tròn lượng giác xác định bởi hai góc đối nhau (H1.12a).

a) Có nhận xét gì về vị trí của hai điểm M, N đối với hệ trục Oxy. Từ đó rút ra liên hệ giữa cos(−α) và cosα;sin(−α)

và sinα

b) Từ kết quả HĐ6a, ta có liên hệ giữa: tan(−α) và tanα;cot(−α) và cotα;

Lời giải:

a) Giả sử M(x_M;y_M),N(x_N;y_N).

Từ Hình 1.12a, ta thấy hai điểm M và N đối xứng với nhau qua trục hoành Ox, do đó ta có: x_M=x_N và y_M=–y_N.

Theo định nghĩa giá trị lượng giác của một góc, ta lại có:

cosα = x_M và cos(–α) = x_N. Suy ra cos (– α) = cos α.

sinα = y_M và sin(–α) = y_N. Suy ra sin α = – sin (– α) hay sin (– α) = – sin α.

b) Ta có: 

tan(−α) = sin(−α) / cos(−α) = −sinα / cosα = −sinα / cosα = −tanα
cot(−α) = cos(−α) / sin(−α) = cosα / −sinα = −cosα/sinα = −cotα
Vậy  tan(−α) = −tanα 

        cot(−α)=−cotα

Giải Toán 11 trang 15

Luyện tập: Tính

a) sin (−675^∘);
b) tan 15π/4;

Lời giải:

sin(−675^∘) = sin(45^∘−2.360^∘) 

                  = sin45^∘

                        = √2/2

tan15π/4 = tan(3π+3π/4)
                = tan(π+3π/4) 

                = tan(3π/4) 

                =tan(π−π/4)

                =−tan(π/4)

                = −1