Giải Toán 11 Kết nối tri thức: Bài 4: Phương trình lượng giác cơ bản

Hướng dẫn Giải Toán 11 Kết nối tri thức Bài 4: Phương trình lượng giác cơ bản ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 11 trang 31

Hoạt động 1:  Nhận biết khái niệm hai phương trình tương đương

Cho hai phương trình 2x – 4 = 0 và (x – 2)(x² + 1) = 0.

Tìm và so sánh tập nghiệm của hai phương trình trên.

Lời giải:

+) 2x – 4 = 0 <=> x = 2.

Vậy tập nghiệm của phương trình 2x – 4 = 0 là S₁ = {2}.(i)

+) (x – 2)(x² + 1) = 0

  x² ≥ 0 với mọi x ∈ R nên x² + 1 > 0 với mọi x ∈ R.

=>  (x – 2)(x² + 1) = 0 khi x – 2 = 0 hay x = 2.

Vậy tập nghiệm của phương trình (x – 2)(x² + 1) = 0 là S₂ = {2}.(ii)

Qua (i) (ii) ta thấy rằng: S1 = S2 = {2}. Hai phương trình trên có cùng một tập nghiệm.

Giải Toán 11 trang 32

Luyện tập 1: Xét sự tương đương của hai phương trình sau: x − 1/x + 1 = 0 và x² − 1 = 0

Lời giải:

+) Ta có: x − 1/x + 1 = 0, điều kiện x ≠ – 1.

               x − 1/x + 1 = 0 

                <=>  x – 1 = 0 

                 <=> x = 1 (thỏa mãn).

Vậy tập nghiệm của phương trình x − 1/x + 1 = 0 là S₁ = {1}.(i)

+) Phương trình x² − 1 = 0 <=> x² = 1 

                                           <=> x = 1 hoặc x = – 1

 Vậy tập nghiệm của phương trình x² − 1=0 là S₂ = {– 1; 1}.(ii)

Qua (i) (ii) ta thấy S1 ≠ S2, vậy hai phương trình đã cho không tương đương.

Hoạt động 2:  Nhận biết công thức nghiệm của phương trình sin x = 1/2

a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoản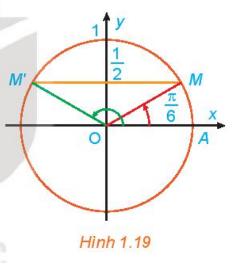g [0; 2π).

b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.

Lời giải:

a) Từ Hình 1.19, ta thấy đường thẳng  y = 1/2 cắt đường tròn tại 2 điểm M, M’. Điểm M biểu diễn góc π/6 và điểm  M' biểu biễn góc π − π/6 = 5π/6.

Vậy trong nửa khoảng [0; 2π), phương trình sinx = 1/2 có hai nghiệm là x = π/6 và x = 5π/6

b) Vì hàm số sin có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là x = π/6 + k2π, k ∈ Z và x = 5π/6 + k2π, k ∈ Z .

Giải Toán 11 trang 34

Luyện tập 2:  Giải các phương trình sau:

a) sin x = √2/2
b) sin 3x = – sin 5x.

Lời giải:

a) sin x = √2/2 <=> sin x = sin π/4

<=>   x = π/4 + k2π hoặc  x = π − π/4 + k2π (k ∈ Z) 

<=>   x = π/4 + k2π hoặc x = 3π/4 + k2π (k ∈ Z)

Vậy phương trình sin x = √2/2 có các nghiệm là x = π/4 + k2π, k ∈ Z và x = 3π/4 + k2π, k ∈ Z

b)    sin 3x = – sin 5x

<=> sin 3x = sin (– 5x)

<=>   3x = −5x + k2π hoặc 3x = π − (− 5x) + k2π (k ∈ Z)

<=>   3x = −5x + k2π hoặc 3x = π + 5x + k2π (k ∈ Z)

<=>   8x = k2π hoặc −2x = π + k2π (k ∈ Z)

 <=>    x = kπ4 hoặc    x  = − π/2 + kπ (k ∈ Z)

Vậy phương trình đã cho có các nghiệm là x = kπ/4 (k ∈ Z) và x = − π/2 + kπ(k ∈ Z)

Hoạt động 3: Nhận biết công thức nghiệm của phương trình cos x = − 1/2

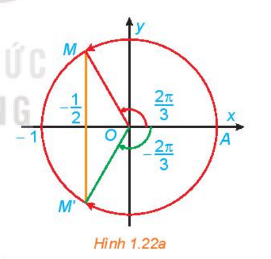
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng [– π; π).

b) Dựa vào tính tuần hoàn của hàm số côsin, hãy viết công thức nghiệm của phương trình đã cho.

 Lời giải:

a) Từ Hình 1.22a, ta thấy đường thẳng  y =  −1/2 cắt đường tròn tại 2 điểm M, M’. Điểm M biểu diễn góc 2π/3 và điểm  M' biểu biễn góc  − 2π/3.

Vậy trong nửa khoảng [ − π; π), phương trình cos x =  −1/2 có hai nghiệm là x = 2π/3 và x =  − 2π/3.

b) Vì hàm số sin có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là x = 2π/ + k2π, k ∈ Z và x =  − 2π/3 + k2π, k ∈ Z .

Giải Toán 11 trang 35

Luyện tập 3: Giải các phương trình sau:

a) 2cosx = –√2 

b) cos3x – sin5x = 0

Lời giải:

a) 2cosx = −√2   <=> cosx = −√2/2 

                           <=> cosx = cos3π/4

                           <=> x = 3π/4 + k2π hoặc x = −3π/4 + k2π (k ∈ Z)

Vậy phương trình đã cho có các nghiệm là x = 3π/4 + k2π (k ∈ Z) và x = −3π/4 + k2π (k ∈ Z)

b) cos3x − sin5x = <=> cos3x = sin5x 

                              <=> cos3x = π/2 − 5x + k2π hoặc 3x = −(π/2 − 5x) + k2π (k ∈ Z)

                              <=> 8x = π/2 + k2π hoặc 2x = π/2 + k2π (k ∈ Z)

                              <=> x = π/16 + kπ/4 hoặc x = π/4 + kπ     (k ∈ Z)

Vậy phương trình có nghiệm là x = π/16 + kπ/4(k ∈ Z) và  x = π/4 + kπ (k ∈ Z)

Vận dụng: Khi Mặt Trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng

một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt

Trời, Trái Đất và Mặt Trăng là α (0° ≤ α ≤ 360°) thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bởi công thức

                                                                F = 1/2(1 − cosα)

                                                                                                                                     (Theo trang usno.navy.mil).

Xác định góc α tương ứng với các pha sau của Mặt Trăng:

a) F = 0 (trăng mới);

b) F = 0,25 (trăng lưỡi liềm);

c) F = 0,5 (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng);

d) F = 1 (trăng tròn).

Lời giải:

a)  F = 0, ta có:

                 1/2(1 − cosα) = 0 

         <=>  cos α = 1 

         <=>  α = k2π  (k ∈ Z)

b)  F = 0,25, ta có:

                  1/2(1 − cosα) = 0,25 

          <=> cosα = 1/2

          <=> cosα = cosπ/3

          <=> α = π/3 + k2π hoặc α = − π/3 + k2π (k ∈ Z)

c)  F = 0,5, ta có:

                  1/2(1 − cosα) = 0.5 

           <=> cos α = 0 

           <=> α = π/2 + kπ  (k ∈ Z).

d) F = 1, ta có:

                  1/2(1 − cosα) = 1

           <=> cos α = – 1 

            <=>  α = π + k2π  (k ∈ Z)

Giải Toán 11 trang 36

Hoạt động 4: Nhận biết công thức nghiệm của phương trình tan x = 1

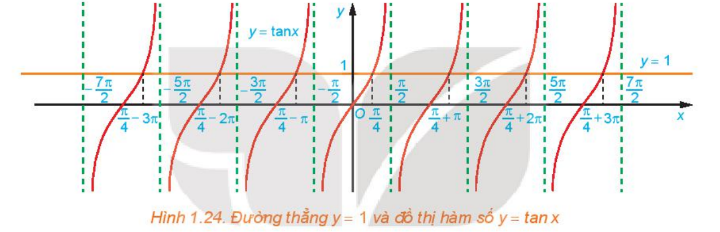
a) Quan sát Hình 1.24, hãy cho biết đường thẳng y = 1 cắt đồ thị hàm số y = tan x tại mấy điểm trên khoảng 

(− π/2 ; π/2)?

b) Dựa vào tính tuần hoàn của hàm tan, hãy viết công thức nghiệm của phương trình đã cho.

Lời giải:

a)  Từ Hình 1.24, ta thấy đường thẳng y = 1 cắt đồ thị hàm số y = tan x tại 1 điểm, điểm này có hoành độ x = π/4

trên khoảng từ (− π/2 ; π/2).

b) Do hàm số tang có tính tuần hoàn và có chu kì là π, nên công thức nghiệm của phương trình tan x = 1 là 

                                                         x = π/4 + kπ (k ∈ Z)

Luyện tập 4: Giải các phương trình sau:

a) √3 tan2x = −1

b)  tan 3x + tan 5x = 0.

Lời giải:

a)   √3 tan2x = −1

<=> tan2x = − 1/√3

<=> tan2x = tan(− π/6)

<=> 2x = − π/6 + kπ/2 (k∈ Z)

<=> x = − π/12 + kπ/2 (k ∈ Z)

Vậy nghiệm của phương trình đã cho là x = −π/12 + kπ/2(k ∈ Z)

b) tan 3x + tan 5x = 0   <=> tan 3x = – tan 5x

                                     <=> tan 3x = tan (– 5x)

                                     <=> 3x = – 5x + kπ (k ∈ Z)

                                     <=> 8x = kπ (k ∈ Z)

                                     <=> x = kπ/8  (k ∈ Z)

Vậy nghiệm của phương trình đã cho là  x = kπ/8 (k ∈ Z)

Giải Toán 11 trang 37

Hoạt động 5: Nhận biết công thức nghiệm của phương trình cot x = – 1

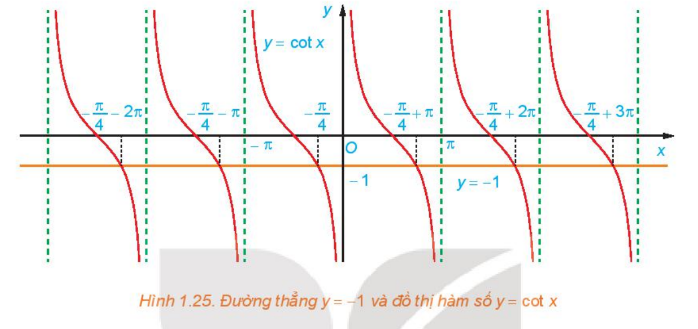
a) Quan sát Hình 1.25, hãy cho biết đường thẳng y = – 1 cắt đồ thị hàm số y = cot x tại mấy điểm trên khoảng

 (0; π)?

b) Dựa vào tính tuần hoàn của hàm côtang, hãy viết công thức nghiệm của phương trình đã cho.

Lời giải:

a)  Từ Hình 1.25, ta thấy đường thẳng y = − 1 cắt đồ thị hàm số y = cot x tại 1 điểm, điểm này có hoành độ 

  x = − π/4 + π = 3π/4 trong khoảng (0; π).

b) Do hàm số tang có tính tuần hoàn và có chu kì là π, nên công thức nghiệm của phương trình tan x = − 1 là

                                                        x = 3π/4 + kπ (k ∈ Z)

Luyện tập 5: Giải các phương trình sau:

a) cot x = 1;

b) √3 cotx + 1 = 0

Lời giải:

a) cot x = 1  <=> cot x = cot π/4

                    <=> x = π/4 + kπ, k ∈ Z.

b) √3 cot x + 1 = 0 <=> cot x = − 1/√3

                              <=> cot x = cot(− π/3)

                              <=> x = − π/3 + kπ, k ∈ Z.

Giải Toán 11 trang 38

Luyện tập 6: Sử dụng máy tính cầm tay, tìm số đo độ và rađian của góc α, biết:

a) cos α = – 0,75;

b) tan α = 2,46;

c) cot α = – 6,18.

Lời giải: Sử dụng máy tính cầm tay ta sẽ tính được kết quả như sau:

a) cos α = – 0,75;

   <=> α ≈ 138°35'26".

   <=> α ≈ 2,41886 rad.

b) tan α = 2,46;

   <=> α ≈ 67°52'41".

   <=> α ≈ 1,1847 rad.

c) cot α = – 6,18.

   <=> α ≈ – 9°11'30".

   <=> α ≈ – 0,16042 rad.