Giải Toán 11 Kết nối tri thức: Bài 3: Hàm số lượng giác
Hướng dẫn Giải Toán 11 Kết nối tri thức Bài 3: Hàm lượng giác ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.
Giải Toán 11 trang 22
Hoạt động 1: Hoàn thành bảng sau:
| x | sin x | cos x | tan x | cot x |
|---|---|---|---|---|
| π/6 | ? | ? | ? | ? |
| 0 | ? | ? | ? | ? |
| −π/2 | ? | ? | ? | ? |
Lời giải: Hoàn thành bảng giá trị:
| x | sin x | cos x | tan x | cot x |
|---|---|---|---|---|
| π/6 | 1/2 | √3/2 | √3/3 | √3 |
| 0 | 0 | 1 | 0 | không xác định |
| −π/2 | −1 | 0 | không xác | 0 |
Giải Toán 11 trang 23
Luyện tập 1: Tìm tập xác định của hàm số y = 1/sinx
Lời giải:
Hàm số y = 1/sinx có nghĩa khi sin x ≠ 0, tức là x ≠ kπ (k ∈ Z).
Vậy tập xác định của hàm số y = 1/sinx là R\ {kπ | k ∈ Z}.
Hoạt động 2: Cho hai hàm số f(a) = x2 và g(x) = x3, với các đồ thị như hình dưới đây
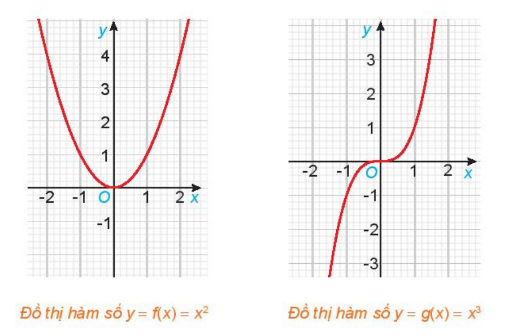
a) Tìm các tập xác định D1, Dg của các hàm số f(x) và g(x)
b) Chứng tỏ rằng f(−x) = f(x), ∀x ∈ Dg. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = g(x) đối với hệ trục tọa độ Oxy?
Lời giải:
a) Biểu thức x2 và x3 luôn có nghĩa với mọi x ∈ R
=> Tập xác định của hàm số f(x) = x2 là Df = R
=> Tập xác định của hàm số g(x) = x3 là Dg = R
b) ∀ x ∈ Df, ta luôn có f(–x) = (–x)2 = x2 = f(x).
=> f(– x) = f(x), ∀ x ∈ Df.
Từ hình vẽ ta có: đồ thị hàm số f(x) = x2 đối xứng với nhau qua trục tung Oy.
c) ∀ x ∈ Dg ta luôn có g(–x) = (–x)3 = –x3 = –g(x).
Vậy g(– x) = – g(x), ∀ x ∈ Dg.
Từ hình vẽ ta thấy đồ thị hàm số g(x) = x3 nhận gốc tọa độ O làm tâm đối xứng.
Giải Toán 11 trang 24
Luyện tập 2: Xét tính chẵn, lẻ của hàm số g(x) = 1/x
Lời giải:
Biểu thức 1/x có nghĩa khi x ≠ 0.
=> tập xác định của hàm số g(x) = 1/x là D = R \ {0}.
Khi x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
g(– x) = 1/−x= −1/x = – g(x), ∀ x ∈ D.
Vậy g(x)= 1/x là hàm số lẻ.
Hoạt động 3: So sánh:
a) sin(x + 2π) và sin x;
b) cos(x + 2π) và cos x;
c) tan(x + π) và tan x;
d) cot(x + π) và cot x.
Lời giải:
a) Ta có:
sin(x + 2π) = sin[π + (x + π)]
= – sin(x + π)
= – sin(π + x)
= – (– sin x) = sin x.
=> sin(x + 2π) = sinx với mọi x ∈ R
b) Ta có:
cos(x + 2π) = cos[π + (x + π)]
= – cos(x + π)
= – (– cos x)
= cos x.
=> cos(x + 2π) = cosx với mọi x ∈ R
c) Ta có:
tan(x + π) = tan(π + x)
= tan x.
=> tan(x + π) = tanx với mọi x ≠ π/2 + kπ, k ∈ Z
d) Ta có:
cot(x + π) = cot(π + x)
= cot x.
=>cot(x + π) = cotx với mọi x ≠ π/2 + kπ, k∈Z
Câu hỏi : Hàm số hằng f(x) = c (c là hằng số) có phải hàm số tuần hoàn không? Nếu hàm số tuần hoàn thì nó có chu kì không?
Lời giải:
Hàm số hằng f(x) = c (c là hằng số) có tập xác định D = .
Với T ≠ 0 sao cho mọi x ∈ D, ta luôn có:
a) x + T ∈ D và x – T ∈ D;
b) f(x + T) = c = f(x). (vì f(x) là hàm số hằng nên với mọi x thì giá trị của hàm số đều có giá trị bằng c).
=> hàm số hằng f(x) = c (c là hằng số) là hàm số tuần hoàn với chu kì là một số dương bất kì.
Giải Toán 11 trang 25
Luyện tập 3: Xét tính tuần hoàn của hàm số y = tan 2x.
Lời giải:
Biểu thức tan 2x có nghĩa khi 2x ≠ π/2 + kπ, k ∈ Z.
=> x ≠ π/4 + kπ/2, k ∈ Z.
=> hàm số y = tan 2x có tập xác định là D = R \ {π/4 + kπ/2 |k ∈ Z}
Với mọi số thực x, ta có:
x − π/2 ∈ D, x + π/2 ∈ D
tan2 (x + π/2) = tan (2x + π)
= tan 2x
Vậy y = tan 2x là hàm số tuần hoàn.
Hoạt động 4: Cho hàm số y = sin x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = sin x trên đoạn [– π; π] bằng cách tính giá trị của sin x với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của sin x với những x âm.
| x | − π | − 3π/4 | − π/2 | − π/4 | 0 | π/4 | π/2 | 3π/4 | π |
|---|---|---|---|---|---|---|---|---|---|
| sin x | ? | ? | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm M(x; sin x) với x ∈ [– π; π] và nối lại ta được đồ thị hàm số y = sin x trên đoạn [– π; π].
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kì T = 2π, ta được đồ thị của hàm số y = sin x như hình dưới đây.
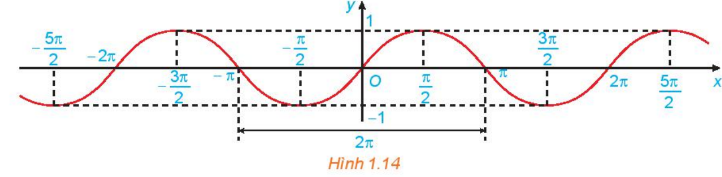
Từ đồ thị ở Hình 1.14, hãy cho biết tập giá trị, các khoảng đồng biến, các khoảng nghịch biến của hàm số y = sin x.
Lời giải:
a) Hàm số y = f(x) = sin x có tập xác định là D = R.
Khi x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
f(– x) = sin (– x) = – sin x = – f(x), ∀ x ∈ D.
=> y = sin x là hàm số lẻ.
b) Hoàn thành bảng giá trị:
| x | − π | − 3π/4 | − π/2 | − π/4 | 0 | π/4 | π/2 | 3π/4 | π |
|---|---|---|---|---|---|---|---|---|---|
| sin | 0 | − √2/2 | − 1 | √2/2 | 0 | √2/2 | 1 | −√2/2 | 0 |
c) Hàm số y = sinx có: - tập xác định là R
- tập giá trị là [-1;1]
- đồng biến trên mỗi khoảng(−π/2 + k2π; π/2 + k2π)
- nghịch biến trên mỗi khoảng (π/2 + k2π; 3π/2 + k2π), k ∈ Z.
Giải Toán 11 trang 26
Luyện tập 4: Tìm tập giá trị của hàm số y = 2sin x.
Lời giải:
Ta có: – 1 ≤ sin x ≤ 1 với mọi x ∈ R.
=> 2.(–1) ≤ 2sinx ≤ 2.1
<=> – 2 ≤ 2sin x ≤ 2 với mọi x ∈ R.
Vậy hàm số y = 2sin x có tập giá trị là T = [– 2; 2].
Vận dụng 1: Xét tình huống mở đầu.
a) Giải bài toán ở tình huống mở đầu.
b) Biết rằng quá trình hít vào xảy ra khi v > 0 và quá trình thở ra xảy ra khi v < 0.
Trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm nào thì người đó hít vào? người đó thở ra?
Lời giải:
a) Chu ký hô hấp: T = 2π/ω = 2π/π3 = 6 (s)
Số chu kỳ hô hấp trong 1 phút là 60/6 = 10 (chu kì).
b) Ta có: v = 0,85sinπt/3
i) v < 0 khi 0.85sinπt/3 > 0
<=> sinπt/3 > 0
Mà −1 ≤ sinπt/3 ≤ 1 với mọi x ∈ R.
Vậy, 0 < sinπt/3 ≤ 1
ii) v < 0 khi 0.85sinπt/3 < 0
<=> sinπt/3<0
Mà – 1 ≤ sinπt/3 ≤ 1 với mọi x ∈ R.
Vậy, −1 ≤ sinπt/3 < 0
Với t ∈ (0; 3) ta có 0 < sinπt/3 ≤ 1
Với t ∈ (3; 5] ta có −1 ≤ sinπt/3 < 0
Vậy: trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm sau 0 giây đến trước 3 giây thì người đó hít vào
trong khoảng thời điểm sau 3 giây đến 5 giây thì người đó thở ra.
Hoạt động 5: Cho hàm số y = cos x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = cos x trên đoạn [– π; π] bằng cách tính giá trị của cos x với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của cos x với những x âm.
| x | − π | − 3π/4 | − π/2 | − π/4 | 0 | π/4 | π/2 | 3π/4 | π |
|---|---|---|---|---|---|---|---|---|---|
| sin | ? | ? | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm M(x; cos x) với x ∈ [– π; π] và nối lại ta được đồ thị hàm số y = cos x trên đoạn [– π; π].
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kì T = 2π, ta được đồ thị của hàm số y = cos x như hình dưới đây.
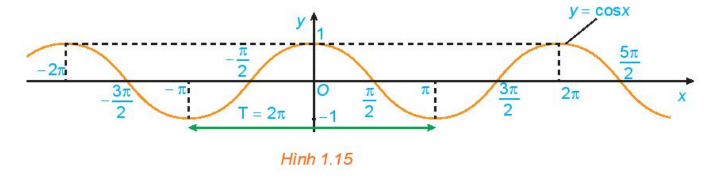
Từ đồ thị ở Hình 1.15, hãy cho biết tập giá trị, các khoảng đồng biến, các khoảng nghịch biến của hàm số y = cos x.
Lời giải:
a) Hàm số y = f(x) = cos x có tập xác định là D = R.
Khi x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
f(– x) = cos (– x) = cos x = f(x), ∀ x ∈ D.
Vậy y = cos x là hàm số chẵn.
b)
| x | − π | − 3π/4 | − π/2 | − π/4 | 0 | π/4 | π/2 | 3π/4 | π/4 |
|---|---|---|---|---|---|---|---|---|---|
| sin x | 0 | − √2/2 | − 1 | √2/2 | 0 | √2/2 | 1 | −√2/2 | 0 |
c) Hàm số y = x có: - tập xác định là R
- tập giá trị là [-1;1]
- đồng biến trên mỗi khoảng(−π + k2π; k2π)
- nghịch biến trên mỗi khoảng (k2π; π + k2π), k ∈ Z.
Giải toán 11 trang 27
Luyện tập 5: Tìm tập giá trị của hàm số y = – 3cos x.
Lời giải:
Ta có: – 1 ≤ cos x ≤ 1 với mọi x ∈ R.
=> (–3).(–1) ≥ –3cosx ≥ (–3).1
<=> – 3 ≤ – 3cos x ≤ 3 với mọi x ∈ R.
Vậy hàm số y = – 3cos x có tập giá trị là [– 3; 3].
Vận dụng 2: Trong Vật lí, ta biết rằng phương trình tổng quát của một vật dao động điều hòa cho bởi công thức x(t) = Acos(ωt + φ), trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời điểm t, A là biên độ dao động (A > 0), ωt + φ là pha của dao động tại thời điểm t và φ ∈ [–π; π] là pha ban đầu của dao động. Dao động điều hòa này có chu kì T = 2π/ω (tức là khoảng thời gian để vật thực hiện một dao động toàn phần).
Giả sử một vật dao động điều hòa theo phương trình x(t) = – 5cos 4πt (cm).
a) Hãy xác định biên độ và pha ban đầu của dao động.
b) Tính pha của dao động tại thời điểm t = 2 (giây). Hỏi trong khoảng thời gian 2 giây, vật thực hiện được bao nhiêu dao động toàn phần?
Lời giải:
a) Phương trình x(t) = – 5cos 4πt (cm)
= 5cos(4πt + π).(cm)
Vậy, biên độ dao động A = 5; pha ban đầu φ = π.
b) Pha của dao động tại thời điểm t = 2 (giây) là ωt + φ = 4π . 2 + π = 9π.
Dao động điều hòa có chu kì: T = 2π/ω
= 2π/4π
= 1/2
= 0.5
Khoảng thời gian để vật thực hiện một dao động toàn phần là 0,5 giây.
Trong khoảng thời gian 2 giây, vật thực hiện được 2 / 0,5 = 4 dao động toàn phần.
Giải Toán 11 trang 28
Hoạt động 6: Cho hàm số y = tan x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = tan x trên khoảng (−π/2; π/2)
| x | − π/3 | −π/4 | −π/6 | 0 | π/6 | π/4 | π/3 |
|---|---|---|---|---|---|---|---|
| y = tan x | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm M(x; tan x) với x ∈ (−π/2; π/2) và nối lại ta được đồ thị hàm số y = tan x trên khoảng (−π/2; π/2)
c) Bằng cách làm tương tự câu b cho các khoảng khác có độ dài bằng chu kì T = π, ta được đồ thị của hàm số y = tan x như hình dưới đây.
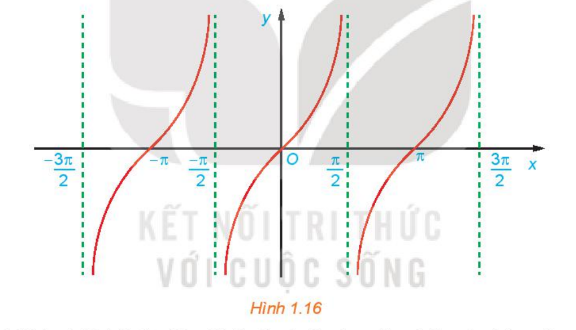
Từ đồ thị ở Hình 1.16, hãy tìm tập giá trị và các khoảng đồng biến của hàm số y = tan x.
Lời giải:
a) Hàm số y = f(x) = tan x có tập xác định là D = R \ {π/2 + kπ |k ∈ Z}.
Khi x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
f(– x) = tan (– x) = – tan x = – f(x), ∀ x ∈ D.
Vậy y = tan x là hàm số lẻ.
b) Hoàn thành bảng giá trị của hàm số y = tan x.
| x | − π/3 | − π/4 | − π/6 | 0 | π/6 | π/4 | π/3 |
|---|---|---|---|---|---|---|---|
| y = tan x | − √3 | − 1 | −√3/3 | 0 | √3/3 | 1 | √3 |
c) Hàm số y = tan x có:
+) Tập giá trị là R \ {π/2 + kπ |k ∈ Z}.
+) Đồng biến trên mỗi khoảng (−π/2 + kπ; π/2 + kπ), k ∈ Z (do đồ thị hàm số đi lên từ trái sang phải trên mỗi khoảng này).
Giải Toán 11 trang 29
Luyện tập 6: Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn [− π; 3π/2] để hàm số y = tan x nhận giá trị âm.
Lời giải:
Khi đồ thị hàm số nằm bên dưới trục hoành thì hàm số y = tan x nhận giá trị âm.
Từ đồ thị đã vẽ ở Hình 1.16 ta thấy trên đoạn [− π; 3π/2] thì y < 0 khi x ∈ (− π/2; 0)∪(π/2; π).
Hoạt động 7: Cho hàm số y = cot x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = cot x trên khoảng (0; π).
| x | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 |
|---|---|---|---|---|---|---|---|
| y = cot x | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm M(x; cot x) với x ∈ (0; π) và nối lại ta được đồ thị hàm số y = cot x trên khoảng (0; π).
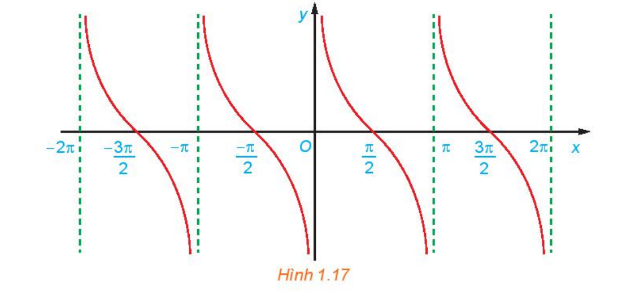
c) Bằng cách làm tương tự câu b cho các khoảng khác có độ dài bằng chu kì T = π, ta được đồ thị của hàm số y =
cot x như hình dưới đây.
Lời giải:
a) Hàm số y = f(x) = cot x có tập xác định là D = R\ {kπ |k ∈ Z}.
Khi x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
f(– x) = cot (– x) = – cot x = – f(x), ∀ x ∈ D.
Vậy y = cot x là hàm số lẻ.
b) Hoàn thành bảng giá trị:
| x | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | π/6 |
|---|---|---|---|---|---|---|---|
| y = cot x | √3 | 1 | √3/3 | 0 | − √3/3 | − 1 | −√3 |
c) Hàm số y = tan x có:
+) Tập giá trị là R\ {kπ |k ∈ Z}.
+) Nghịch biến trên mỗi khoảng (kπ; π + kπ), k ∈ Z (do đồ thị hàm số đi lên từ phải sang trái trên mỗi khoảng này).
Giải Toán 11 trang 30
Luyện tập 7: Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn [−π/2; 2π] để hàm số y = cot x nhận giá trị dương.
Lời giải:
Khi đồ thị ở trên trục hoành thì hàm số y = cot x nhận giá trị dương
Từ đồ thị ở Hình 1.17 ta suy ra trên đoạn [−π/2; 2π] thì y > 0 khi x ∈ (0; − π/2)∪(π; 3π/2)

