Bài 10: Đường thẳng và mặt phẳng trong không gian

Hướng dẫn Giải Toán 11 Kết nối tri thức Bài 10: Đường thẳng và mặt phẳng trong không gian ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 11 trang 71

Câu hỏi: Hãy tìm một số hình ảnh mặt phẳng trong thực tế

Lời giải: 

mặt bảng:

mặt hồ:

Hoạt động 1: Chấm phạt đền trên sân bóng đá cho ta hình ảnh về một điểm thuộc một mặt phẳng. Hãy tìm thêm

các ví dụ khác cũng gợi cho ta hình ảnh đó.

Lời giải: 

Cái nắm cửa  cho ta hình ảnh về một điểm thuộc một mặt phẳng

Giải Toán 11 trang 72

Hoạt động 2:  Chiếc xà ngang đặt tựa lên hai điểm A, B của trụ nhảy thể hiện hình ảnh của một đường thẳng đi

qua hai điểm đó. Có thể tìm được một đường thẳng khác cũng đi qua hai điểm A, B hay không?

Lời giải: 

Không thể tìm được một đường thẳng khác cũng đi qua hai điểm A, B

Vì qua 2 điểm phân biệt chỉ có duy nhất 1 đường thẳng đi qua

Câu hỏi:  Có bao nhiêu đường thẳng đi qua hai trong số ba điểm không thẳng hàng

Lời giải: 

Với mỗi 2 điểm phân biệt sẽ có duy nhất một đường thẳng đi qua.

Như vậy, với 3 điểm không thẳng hàng sẽ tạo thành 3 cặp điểm phân biệt nên sẽ có 3 đường thẳng đi qua 2 trong

số 3 điểm đó

Hoạt động 3: Trong Hình 4.4 là một khối rubik có bốn đỉnh và bốn mặt, mỗi mặt là một tam giác

a) Đặt khối rubik sao cho ba đỉnh của mặt màu đỏ đều nằm trên mặt bàn. Khi đó, mặt màu đỏ của khối rubik có

nằm trên mặt bàn hay không?

b) Có thể đặt khối rubik sao cho bốn đỉnh của nó đều nằm trên mặt bàn hay không?

Lời giải: 

a) Vì 3 đỉnh của mặt màu đỏ đều nằm trên mặt bàn nên mặt màu đỏ cũng nằm trên mặt bàn

b) Không thể đặt khối rubik sao cho bốn đỉnh của nó đều nằm trên mặt bàn vì bốn đỉnh của rubik không cùng thuộc

một mặt phẳng

Câu hỏi: Có bao nhiêu mặt phẳng đi qua ba điểm thẳng hàng?

Lời giải: 

Có vô số mặt phẳng đi qua ba điểm thẳng hàng

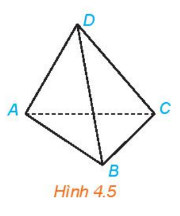
Luyện tập 1:  Cho tứ giác ABCD. Có bao nhiêu mặt phẳng đi qua ba trong số bốn đỉnh của tứ giác đó?

Lời giải:

Có 4 mặt phẳng đi qua ba trong số bốn đỉnh của tứ giác đó là: (DAB), (DAC), (DBC), (ABC).

Vận dụng 1: Hãy giải thích tại sao trong thực tiễn có nhiều đồ vật được thiết kê gồm ba chân như chân đỡ máy

ảnh, giá treo tranh, kiềng ba chân treo nồi,...

Lời giải:

Khi thiết kế các đồ vật gồm ba chân như chân đỡ máy ảnh, giá treo tranh, kiềng ba chân treo nổi,... ta thấy

các đồ vật này có thể đứng thẳng mà không bị đổ trên các bề mặt bởi vì các ba chân của các đồ vật này giống

như 3 điểm không thẳng hàng tạo thành mặt phẳng cố định giúp giá đỡ được chắc chắn hơn.

Giải Toán 11 trang 73

Hoạt động 4: Căng một sợi dây sao cho hai đầu của sợi dây nằm trên mặt bàn. Khi đó, sợi dây có nằm trên mặt

bàn hay không?

Lời giải: 

Vì hai đầu của sợi dây là hai điểm thuộc sợi dây đó nằm trên mặt bàn nên sợi dây đó cũng nằm trên mặt bàn.

Luyện tập 2:  Trong Ví dụ 2, lấy điểm N thuộc đường thẳng AB sao cho N khác M. Đường thẳng MN có thuộc mặt

phẳng (ABC) hay không?

Lời giải:

Đường thẳng MN có hai điểm phân biệt M, N thuộc mặt phẳng (ABC) nên đường thẳng MN nằm trong mặt phẳng (ABC).

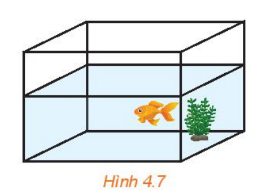
Hoạt động 5: Trong Hình 4.7, mặt nước và thành bể có giao nhau theo đường thẳng hay không?

Lời giải:

Mặt nước và thành bể có giao nhau theo đường thẳng đi qua các điểm chung.

Giải Toán 11 trang 74

Luyện tập 3:  Trong ví dụ 3, hãy xác định giao tuyến của hai mặt phẳng (SBM) và (SCN)

Lời giải:

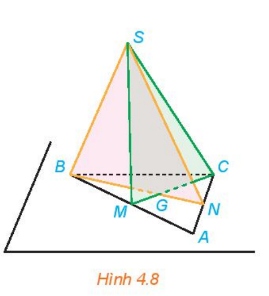
Vì A là giao điểm của BM và CN nên A nằm trên cả hai mặt phẳng (SBM) và (SCN).

S, A là hai điểm chung của hai mặt phẳng (SBM) và (SCN) nên giao tuyến của hai mặt phẳng này là đường thẳng

SA.

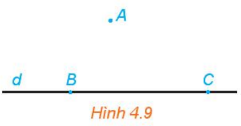
Hoạt động 6: Cho đường thẳng d và điểm A không thuộc d. Trên đường thẳng d lấy ha điểm phân biệt B, C

(H.4.9). Mặt phẳng (ABC) có chứa điểm A và đường thẳng d hay không? Mặt phẳng (ABC) có chứa hai đường

thẳng AB và BC hay không?

Lời giải:

Quan sát Hình 4.9 ta thấy mặt phẳng (ABC) chứa điểm A và đường thẳng d.

Vì vậy mp(ABC) cũng chứa hai đường thẳng AB và BC.

Giải Toán 11 trang 75

Luyện tập 4: Trong Ví dụ 4, vẽ một đường thẳng c cắt cả hai đường thẳng a và b. Xác định giao tuyến của hai mặt phẳng: mp(S,a) và mp(S,c); mp(S,b) và mp(S,c)

Lời giải:

Đường thẳng c cắt a, b lần lượng tại L và K.

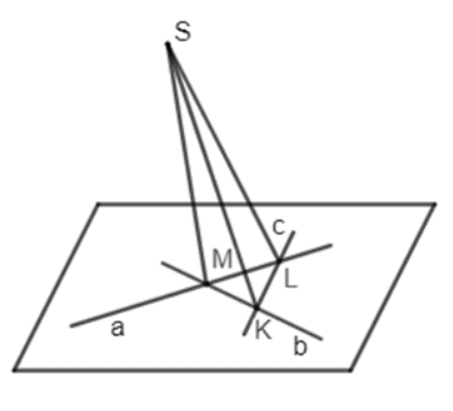
Giao tuyến của mp(S,a) và mp(S,c) là SL vì hai điểm S và L cùng thuộc mp(S, a) và mp(S, c)

Giao tuyến của mp(S,b) và mp(S,c) là SK vì ai điểm S và K cùng thuộc mp(S, b) và mp(S, c)

Vận dụng 2: Để tránh cho cửa ra vào không bị va đập vào các đồ dùng xung quanh (do mở cửa quá mạnh hoặc

do gió to đập cửa), người ta thường sử dụng một phụ kiện là hít cửa nam châm. Hãy giải thích tại sao khi của

được hút tới vị trí của nam châm thì cánh cửa được giữ cố định.

Lời giải: 

Phụ kiện hít cửa nam châm đại diện cho 1 điểm cố định, một cạnh của cánh cửa đại diện cho một đường thẳng không chứa điểm phụ kiện hít cửa nam châm.

Có một mặt phẳng được xác định khi phụ kiện hít cửa và một cạnh của cánh cửa, khi đó cánh cửa luôn được giữa cố định.

Hoạt động 7: Các hình ảnh dưới đây có đặc điểm chung nào với hình chóp tam giác đều mà em đã học ở lớp 8?

Lời giải:

Các cạnh bên đều bằng nhau.

Các mặt bên của hình chóp này là tam giác cân.

Chân đường cao trung với tâm đáy.

Góc được tạo bởi mặt bên và mặt đáy đều bằng nhau.

Góc được tạo bởi cạnh bên và mặt đáy đều bằng nhau.

Giải Toán 11 trang 76

Luyện tập 5: Cho hình chóp S.ABCD. Gọi tên các mặt bên và mặt đáy của hình chóp đó.

Lời giải:

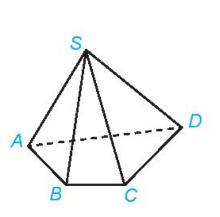
Các mặt bên: SAB, SBC, SCD, SAD

Mặt đáy: ABCD

Hoạt động 8: Trong các hình chóp HĐ7, hình chóp nào có ít mặt nhất? Xác đinh số cạnh và số mặt của hình chóp đó.

Lời giải:

Hình thứ ba có ít mặt nhất. Có 4 mặt và 6 cạnh

Luyện tập 6: Trong Ví dụ 6, xác định giao điểm của đường thẳng DF và mặt phẳng (ABC)

Lời giải:

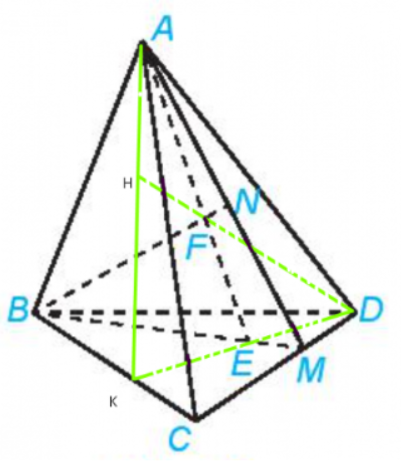
Trong mp(BCD) ta có: DE cắt BC tại K

Trong mp(ADK) ta có: DF cắt AK tại H

Mà AK nằm trong mp(ABC) suy ra H  nằm trong mp(ABC)

Vậy H là giao điểm của DF và mp(ABC)