Giải Toán 8 Kết nối tri thức: Bài 16: Đường trung bình của tam giác

Hướng dẫn Giải Toán 8 Kết nối tri thức Bài 16: Đường trung bình của tam giác ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới

Giải Toán 8 trang 82

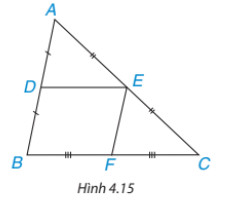
Hoạt động 1: Cho DE là đường trung bình của tam giác ABC (H.4.15)  Sử dụng định lí Thales đảo, chứng minh

rằng DE // BC

Lời giải

Ta có DE là đường trung bình của tam giác ABC nên:

+ D là trung điểm của AB hay AD = 12/AB nên AD/AB = 12;

+ E là trung điểm của AC hay AE = 12/AC nên AE/AC = 12.

Xét tam giác ABC :  AD/AB = AE/AC = 12

 theo định lí Thalès đảo ta có: DE // BC (đpcm).

Hoạt động 2: Cho DE là đường trung bình của tam giác ABC (H.4.15). Gọi F là trung điểm của BC. Chứng minh

tứ giác DEFB là hình bình hành. Từ đó suy ra DE = 12/BC

Lời giải

Ta có:  

F là trung điểm của BC nên BF/BC=12

E là trung điểm của AC nên AE/AC=12

=> BF/BC = AE/AC do đó EF // AB

Xét tứ giác DE/FB ta có: DE // BF, EF // DB 

=> DEFB là hình bình hành ⇒ DE = BF

Mà BF = 12/BC suy ra DE = 12/BC

Giải Toán 8 trang 83

Luyện tập: Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?

Lời giải

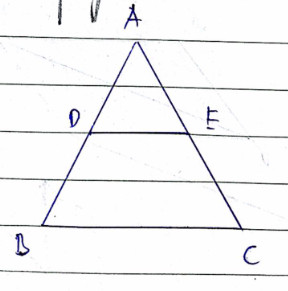
Tam giác ABC cân tại A suy ra ˆB=ˆC.

Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác ABC.

Suy ra DE // BC nên tứ giác DECB là hình thang.

Hình thang DECB có ˆB=ˆC =>  là hình thang cân.