Bài 4.8 trang 83 SGK Toán 8 Tập 1 Kết nối tri thức

Bài 16: Đường trung bình của tam giác

Bài 4.8 trang 83 SGK Toán 8 Tập 1 Kết nối tri thức:

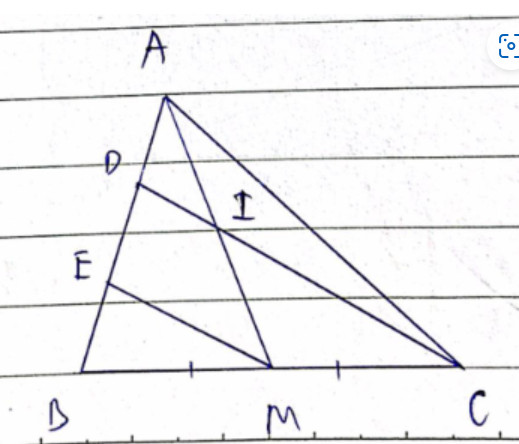
Cho tam giác ABC có trung tuyến AM. Lấy hai điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E

a) Chứng minh DC // EM

b) DC cắt AM tại I. Chứng minh I là trung điểm của AM

Lời giải:

a) Xét ΔBDC ta có:

E là trung điểm của BD (BE=ED; B,E,D thẳng hàng)

M là trung điểm của BC (gt)

Vậy EM là đường trung bình của ΔBDC (Định nghĩa đường trung bình của tam giác)

⇒ ME//CD (Định lí 2 về đường trung bình của tam giác)

b) Xét ΔAEM ta có:

D là trung điểm của AE(AD=DE; A,D,E thẳng hàng)

DI//EM(cmt)

Như vậy: I là trung điểm của AM (Định lí 1 về đường trung bình của tam giác)

=> AI = IM (đpcm)

* Kiến thức vận dụng giải bài tập:

Dựa vào tính chất đường trung bình để chứng minh