Giải Toán 8 Kết nối tri thức: Bài 15: Định lí Thales trong tam giác

Hướng dẫn Giải Toán 8 Kết nối tri thức Bài 15: Định lí Thales trong tam giác ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 8 trang 77

Hoạt động 1: Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài. Với các độ dài

đó hãy tính tỉ số ABCD

Lời giải

Chọn đoạn MN làm đơn vị độ dài thì MN = 1 (đvđd).

Khi đó, AB = 2 (đvđd); CD = 6 (đvđd).

=> AB/CD = 2/6 = 1/3.

Vậy AB = 2 (đvđd); CD = 6 (đvđd); AB /CD = 13.

Hoạt động 2: Dùng thước thẳng, đo độ dài hai đoạn AB và CD (đơn vị: cm) rồi dùng kết quả vừa đo để tính tỉ số

ABCD

Lời giải

Ta đo được độ dài là: AB = 4,8; CD = 14,4 cm

ABCD = 3/9 = 1/3

Hoạt động 3: So sánh tỉ số tìm được trong hai hoạt động trên

Lời giải

Tỉ số AB/CD tìm được ở Hoạt động 1 và Hoạt động 2 bằng nhau (1/3).

Luyện tập 1: Tìm tỉ số của các cặp đoạn thẳng có độ dài như sau:

a) MN = 3 cm và PQ = 9 cm

b) EF = 25 cm và HK = 10 dm

Lời giải

a) Tỉ số của các đoạn thẳng được tính như sau:

MN/PQ = 3/9 = 1/3; PQ/MN = 9/3 = 3/1.

Vậy MNPQ = 1/3; PQMN = 3/1.

b) Ta đổi 10 dm = 100 cm.

Tỉ số của các đoạn thẳng được tính như sau:

EF/HK = 25/100 = 1/4; HK/EF =100/25 = 4/1.

Vậy  EFHK = 1/4; HKEF = 4/1.

Giải Toán 8 trang 78

Luyện tập 2: Cho tam giác ABC và một điểm B' nằm trên cạnh AB. Qua điểm B', ta vẽ một đường thẳng song

song với BC, cắt AC tại C' (H.4.4). Dựa vào hình vẽ, hãy tính và so sánh các tỉ số sau và viết các tỉ lệ thức:

a) AB′AB và AC′AC

b) AB′B′B và AC′C′C

c) B′BAB và C′CAC

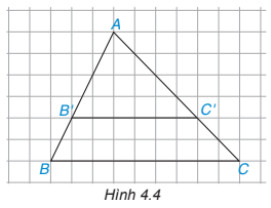
Lời giải

a) Từ hình vẽ ta thấy:

 AB′/AB = 4/6 = 2/3

AC′/AC = 4/6 = 2/3

Ta có tỉ lệ thức AB′/AB=AC′/AC

b) Từ hình vẽ ta thấy:

 AB′/B′B = 4/2 = 2

AC′/C′C = 2

Ta có tỉ lệ thức AB′/B′B = AC′/C′C

c) Từ hình vẽ ta thấy: 

B′B/AB = 1/3

C′C/AC = 1/3

Ta có tỉ lệ thức B′B/AB = C′C/AC

Giải Toán 8 trang 79

Luyện tập 3: Tìm các độ dài x, y trong hình 4.6

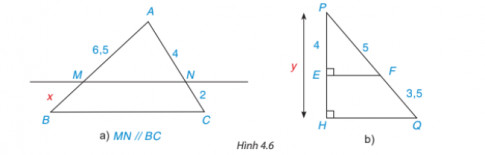
Lời giải

a) Áp dụng định lí Thales vào ∆ABC, ta có:

AM/BM = AN/CN hay 6,5/x = 4/2 = 2

=> x = 6,5.24 = 3,25 (đvđd).

Vậy x = 3,25 (đvđd).

b) Ta có: PQ = PF + QF = 5 + 3,5 = 8,5 (đvđd).

Áp dụng định lí Thales vào ∆PHQ, ta có:

PE/PH = PF/PQ hay 4/y=5/8,5.

=> y = 4.8,55 = 6,8 (đvđd).

Vậy y = 6,8 (đvđd).

Hoạt động 4: Cho ΔABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B', trên cạnh AC lấy điểm C' sao cho

AB' = 4 cm, AC' = 6 cm (H.4.7)

So sánh các tỉ số AB'/AB và AC'/AC.

Vẽ đường thẳng a đi qua B' và song song với BC, đường thẳng a cắt AC tại điểm C''. Tính độ dài đoạn thẳng AC''.

Nhận xét gì về hai điểm C', C'' và hai đường thẳng B'C', BC?

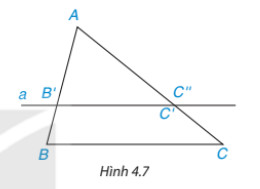
Lời giải

AB′/AB = 4/6 = 2/3

AC′/AC = 6/9 = 2/3

⇒AB′/AB = AC′/AC

B′C′′//BC ⇒ AB′/AB = AC′′/AC ⇒ 4/6 = AC′′/9 ⇒ AC′′ = 6

Trên cạnh AC lấy điểm C’ sao cho AC’ = 6 cm.

Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên điểm C’’ nằm trên cạnh

AC sao cho AC’’ = 6 cm.

Do đó, hai điểm C’, C’’ trùng nhau.

Vì hai điểm C’, C’’ trùng nhau mà B’C’’ // BC nên B’C’ // BC.