Bài 4.4 trang 80 SGK Toán 8 Tập 1 Kết nối tri thức

Bài 15: Định lí Thales trong tam giác

Bài 4.4 trang 80 SGK Toán 8 Tập 1 Kết nối tri thức:

Cho tam giác ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng BM=1/3.BC

Lời giải:

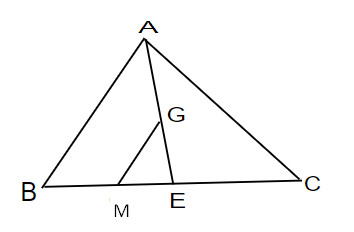
Kẻ AE là đường trung tuyến của tam giác ABC, E ∈ BC

Vì G là trọng tâm của tam giác ABC nên ta có :

 AG=2/3.AE

⇒AG/AE = 2/3

Xét tam giác ABE có GM//AB ( G∈AE; M ∈BE vì M∈BC mà E∈BC) ta có :

BM/BE = AG/AE ( áp dụng định lý Ta-lét ) 

Ta có : AG/AE = 2/3 ( cmt )

⇒ BM/BE=2/3

AE là đường trung tuyến của tam giác ABC ( E ∈BC ) => E là trung điểm của BC

⇒ BE = EC và BE + EC = BC

⇒ BM/BC = BM/BE + EC = 2/2BE = 2/6 = 1/3

⇒ BM=1/3BC (đpcm)

* Kiến thức vận dụng giải bài tập:

Áp dụng tính chất trọng tâm G trong tam giác ABC và định lí Thales vì MG // AB