Giải Toán 8 Kết nối tri thức: Bài 17: Tính chất đường phân giác của tam giác
Hướng dẫn Giải Toán 8 Kết nối tri thức Bài 17: Tính chất đường phân giác của tam giác ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.
Giải Toán 8 trang 84
Hoạt động 1: Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trân tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sư tia phân giác At cắt BC tại điểm D.
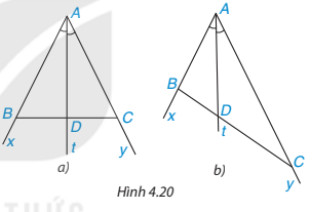
Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh hai tỉ số DBDC và ABAC
Lời giải
Theo đề bài cho, At là tia phân giác của góc xAy hay AD là tia phân giác của góc BAC.
Tam giác ABC cân tại A (vì AB = AC) ta có:
AD là tia phân giác của góc BAC => AD cũng là đường trung tuyến của tam giác ABC.
Suy ra D là trung điểm của cạnh BC hay DB = DC
DB/DC = 1.
Vì AB = AC nên AB/AC = 1.
Vậy khi lấy B và C sao cho AB = AC thì DB/DC = AB/AC.
Hoạt động 2: Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trân tia Ax, điểm C trên tia Ay, ta được
tam giác ABC. Giả sư tia phân giác At cắt BC tại điểm D.
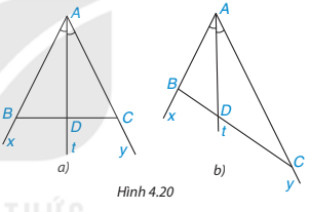
Khi lấy B và C sao cho AB = 2 cm và AC = 4 cm (H.4.20b), hãy dùng thước có vạch chia đến mm để đo độ dài các
đoạn thẳng DB, DC rồi so sánh hai tỉ số DBDC và ABAC
Lời giải
Dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC, ta được:
DB = 11 mm = 1,1 cm và DC = 22 mm = 2,2 cm.
Khi đó, DBDC = 1,1/2,2 = 1/2; AB/AC = 2/4=1/2.
Ta khi lấy B và C để sao cho AB = 2 cm và AC = 4 cm => DB/DC = AB/AC.
Luyện tập: Tính độ dài x trên Hình 4.23.
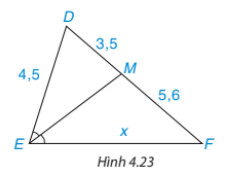
Lời giải
Trong Hình 4.23 có ˆDEM=ˆMEF. EM là tia phân giác của ˆDEF.
Áp dụng tính chất đường phân giác của tam giác, ta có:
ED/EF = MD/MF hay 4,5/x = 3,5/5,6
=> x = 5,6.4,5/3,5 = 7,2 (đvđd)
Như vậy x = 7,2 (đvđd).

