Bài 3.30 trang 72 SGK Toán 8 Tập 1 Kết nối tri thức

Bài 14: Hình thoi và hình vuông 

Bài 3.30 trang 72 SGK Toán 8 Tập 1 Kết nối tri thức: 

Cho tam giác ABC, D là một điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB, AC, chúng cắt các cạnh AC, AB lần lượt tại E, F

a) Tứ giác AEDF là hình gì? Vì sao?

b) Nếu tam giác ABC cân tại A thì điểm D ở vị trí nào trên cạnh BC để tứ giác AEDF là hình thoi?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì?

d) Nếu tam giác ABC vuông cân tại A thì điểm D ở vị tri nào trên cạnh BC để AEDF là hình vuông?

Lời giải:

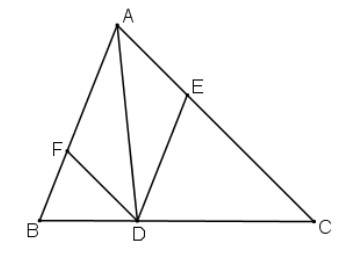
a) DE // AF, DF // AE (gt) 

=> Tứ giác AEDF là hình bình hành.

b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. 

D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.

Mà ABC là tam giác cân tại A 

Suy ra D là trung điểm của BC.

c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).

d) Nếu ABC vuông tại A và D là trung điểm cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

* Kiến thức vận dụng giải bài tập:

Vận dụng vào các tính chất của hình vuông, hình bình hành, hình chữ nhật và hình thoi.