Bài 3.29 trang 71 SGK Toán 8 Tập 1 Kết nối tri thức

Bài 14: Hình thoi và hình vuông 

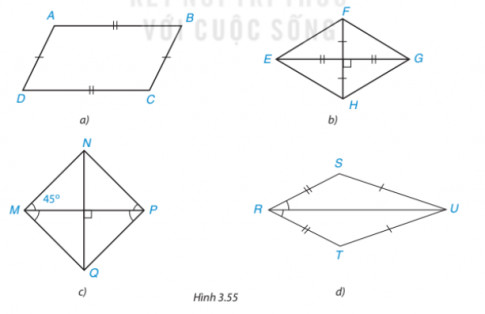
Bài 3.29 trang 71 SGK Toán 8 Tập 1 Kết nối tri thức: Tìm các hình thoi và hình vuông trong Hình 3.55

Lời giải:

- Trong hình 3.55a) có:

Tứ giác ABCD có AB = CD; AD = BC.

=> tứ giác ABCD là hình bình hành.

- Trong hình 3.55b) có:

Tứ giác EFGH có hai đường chéo EG và FH cắt nhau tại trung điểm của mỗi đường.

=> Tứ giác EFGH là hình bình hành.

Hình bình hành EFGH có hai đường chéo vuông góc với nhau

Do đó tứ giác EFGH là hình thoi.

- Trong hình 3.55c) có tam giác MNP có:

góc NMP = góc NPM = 45⁰

⇒ góc MNP = 180⁰ − 45⁰ −45⁰ = 90⁰ (1)

NMP = 45⁰ + 45⁰ = 90⁰ (2)

NPQ = 45⁰ + 45⁰ = 90⁰ (3)

Từ (1), (2) và (3) ta có MNPQ là hình chữ nhật (vì có 3 góc vuông).

Xét hình chữ nhật MNPQ có:

MP⊥NQ => MNPQ là hình vuông 

- Trong hình 3.55d) có:

Tứ giác SRTU là hình cái diều (không phải hình thoi) vì các cạnh của tứ giác không bằng nhau.

* Kiến thức vận dụng giải bài tập:

Dựa vào các dấu hiệu nhận biết hình vuông, hình thoi.