Giải Toán 7 Kết nối tri thức: Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Hướng dẫn Giải Toán 7 Kết nối tri thức Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 7 trang 70

Hoạt động 1: Vẽ góc xAy = 60^∘. Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm, AC = 3 cm. Nối điểm B với điểm C ta được tam giác ABC (H.4.27)

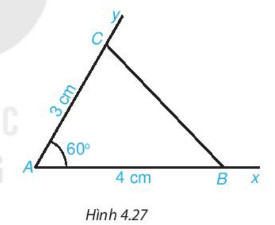
Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.

Lời giải:

Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC ta được kết quả: BC ≈ 3,6 cm

Hoạt động 2: Vẽ thêm tam giác A'B'C' với góc B′A′C′ = 60^∘, A'B' = 4 cm và A'C' = 3 cm (H.4.28).

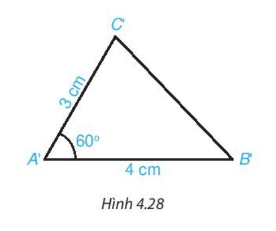
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và A'B'C'.

- Hai tam giác ABC và A'B'C' có bằng nhau không?

- Độ dài các cạnh BC và B'C' của hai tam giác em vừa vẽ có bằng các cạnh AB và A'B' của hai tam giác các bạn khác không?

- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?

Lời giải:

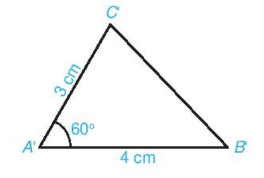
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và A'B'C' :

AB = A'B' = 4cm

AC = A'C' = 3cm

BC = B'C' ≈ 3,6 cm

Xét hai tam giác ABC và A'B'C' ta có:

AB = A'B' 

AC = A'C' 

BC = B'C'
 =>  ΔABC =  ΔA'B'C'

+) Độ dài các cạnh tương ứng của 2 tam giác ABC và A'B'C' bằng nhau.

+) Hai tam giác ABC và A'B'C bằng nhau.

+) Độ dài các cạnh BC và B'C' của hai tam giác em vừa vẽ bằng các cạnh AB và A'B' các bạn khác vẽ. Hai tam giác em vừa vẽ bằng hai tam giác mà các bạn khác vẽ.

Giải Toán 7 trang 71

Câu hỏi:  Trong Hình 4.29, hai tam giác nào bằng nhau?

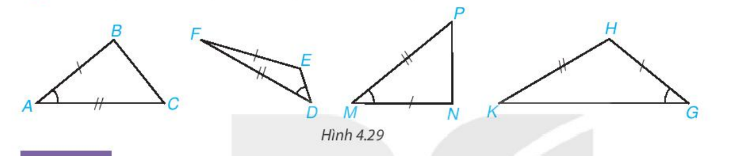
Lời giải:

Xét hai tam giác ABC và MNP có:

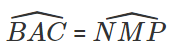
AB = MN

AC = MP

=> ΔABC = ΔMNP(c.g.c)

Hai tam giác ΔDEF và ΔGHK có góc D không phải góc xen giữa hai cạnh EF, FD và góc G không phải góc xen giữa hai cạnh GH, HK nên hai tam giác này ta không xét.

Vậy trong Hình 4.29 có  ΔABC = ΔMNP.

Luyện tập 1: Hai tam giác ABC và MNP trong Hình 431 Có bằng nhau không? Vì sao?

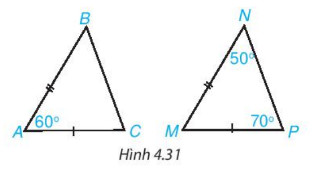
Lời giải:

Xét tam giác MNP ta có:

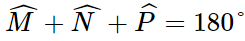
Khi đó:

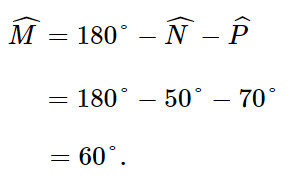
Xét hai tam giác ABC và MNP ta có:

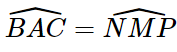
AB = MN

AC = MP

=>  ΔABC = ΔMNP (c. g.c)

Vận dụng: Cho Hình 4.32, biết góc OAB = góc ODC, OA = OD và AB = CD

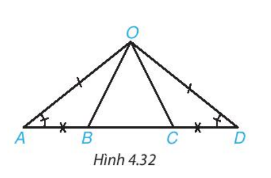
Chứng minh rằng:

a) AC = DB

b) ΔOAC = ΔODB

Lời giải:

a)

Ta có: AB = CD 

mà AC = AB + BC và BD = CD + BC 

=> AC = BD

b) Xét hai tam giác  ΔOAC = ΔODB ta có:

OA = OD

AC = BD

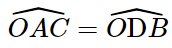
Vậy: ΔOAC = ΔODB

Giải Toán 7 trang 72

Hoạt động 3: Vẽ đoạn thẳng BC = 3cm. Vẽ hai tia Bx và Cy sao cho góc xBC = 80^∘ và góc yBC = 40^∘ như Hình 4.33. Lấy giao điểm A của hai tia Bx và Cy, ta được tam giác ABC (H.4.33)

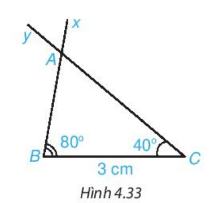
Dùng thước thẳng có vạch chia độ dài hai cạnh AB, AC của tam giác ABC.

Lời giải:

Dùng thước thẳng có vạch chia độ dài hai cạnh AB, AC của tam giác ABC ta được:

AB ≈ 2,2 cm

AC ≈ 3,4 cm

Hoạt động 4: Vẽ thêm tam giác A′B′C′ sao cho B′C′ = 3cm, góc A'B'C' = 80^∘, A'C'B' = 40^∘(H.4.34). Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác ABC và A′B′C′. Hai tam giác ABC và A′B′C′ có bằng nhau không?

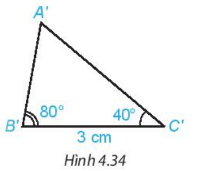
Lời giải:

Dùng thước thẳng có vạch chia hoặc compa đo độ dài các cạnh của hai tam giác ABC và A′B′C′ ta được:

AB = A'B' ≈ 2,2 cm

AC = A'C' ≈ 3,4cm

BC = B'C' = 3cm.

Xét hai tam giác  ABC và A′B′C′ ta có:

AB = A'B'

AC = A'C'

BC = B'C'

=> ΔABC = ΔA'B'C'

Câu hỏi:  Hai tam giác nào trong Hình 4.35 bằng nhau?

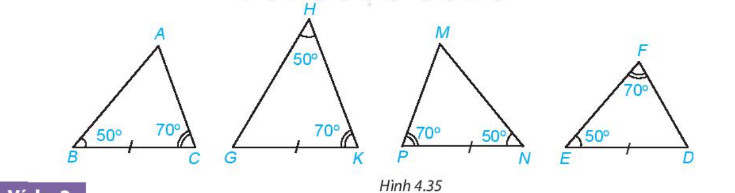
Lời giải:

Xét hai tam giác ABC và MNP ta có:

BC = NP 

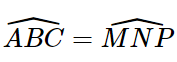
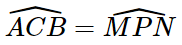
=> ΔABC = ΔMNP (g.c.g).

ΔGHK có góc H không phải góc kề của cạnh GK; ΔDEF có góc F không phải góc kề của cạnh DE nên ta không xét hai tam giác này.

Vậy trong Hình 4.35 có ΔABC = ΔMNP

Giải Toán 7 trang 73

Luyện tập: Chứng minh hai tam giác ABD và CBD trong Hình 4.37 bằng nhau.

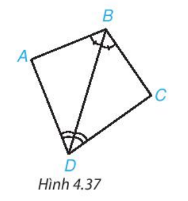
Lời giải:

 Xét hai tam giác ABD và CBD ta có:

BD chung

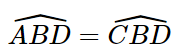
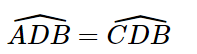
Vậy hai tam giác ABD và CBD trong Hình 4.37 bằng nhau.

Thử thách nhỏ: Bạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao?

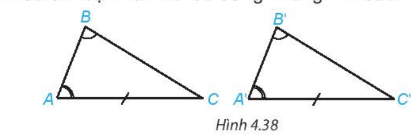
Lời giải:

Bạn Lan nói đúng vì : Tổng ba góc trong một tam giác bằng 180^∘. Mà tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì góc còn lại của hai tam giác cũng bằng nhau:

Vậy: