Bài 4.13 trang 73 SGK Toán 7 Tập 1 Kết nối tri thức

Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 4.13 trang 73 SGK Toán 7 Tập 1 Kết nối tri thức

Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.

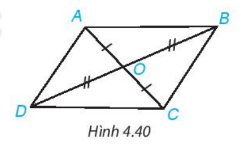
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau;

b) Chứng minh rằng ΔDAB = ΔBCD.

*Lời giải:

a)  Hai cặp tam giác có chung đỉnh O bằng nhau là: ΔAOB và ΔCOD(c – g – c); ΔAOD và ΔCOB (c – g – c)

b) Xét ΔAOB và ΔCOD, ta có :

OC = OA

Góc AOB = góc COD (hai góc đối đỉnh)

OB = OD

Do đó ΔAOB = ΔCOD (c-g-c)

Vậy AB = DC (1)

Xét ΔAOD và ΔCOB, ta có :

AO = CO

Góc AOD = góc COB (hai góc đối đỉnh)

DO = BO

Do đó ΔAOD = ΔCOB (c-g-c) 

Vậy AD = CB (2)

Từ (1) và (2) suy ra ΔDAB và ΔBCD có :

AB = DC

BD chung

AD = CB

Vậy ΔDAB = ΔBCD (c-c-c)

*Kiến thức vận dụng giải bài tập

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.