Giải Toán 8 Kết nối tri thức: Bài 13: Hình chữ nhật

Hướng dẫn Giải Toán 8 Kết nối tri thức Bài 12: Hình chữ nhật ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 8 trang 64

Hoạt động 1: 

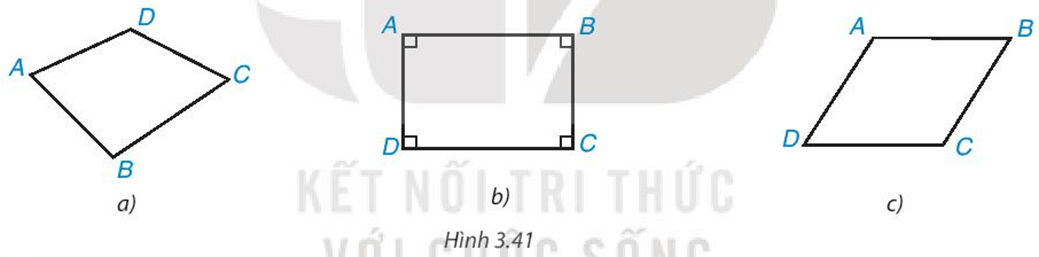
Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?

Lời giải

Tứ giác ABCD trong Hình 3.41b là hình chữ nhật vì có ˆA = ˆB = ˆC = ˆD = 90°.

Tứ giác ABCD trong Hình 3.41a và Hình 3.41c không phải là hình chữ nhật vì không có 4 góc vuông.

Hoạt động 2:

 Hình chữ nhật có là hình bình hành không, có là hình thang cân không? Tại sao?

Lời giải

Hình chữ nhật là hình bình hành vì có các cặp góc đối bằng nhau

Hình chữ nhật là hình thang cân vì có cặp góc ở đáy bằng nhau

Giải Toán 8 trang 65

Luyện tập 1:

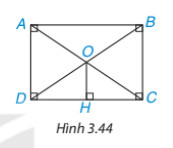
 Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH⊥DC (H.3.44). Chứng minh rằng H là

trung điểm của DC

Lời giải

Vì ABCD là hình chữ nhật có hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.

=> OA = OB = OC = OD.

Xét tam giác OCD cân tại O (vì OC = OD) 

=> OH là đường cao vừa là đường trung tuyến.

Do đó CH = DH.

Vậy H là trung điểm của DC.

Hoạt động 3: Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có là hình chữ nhật

không? Vì sao?

Lời giải

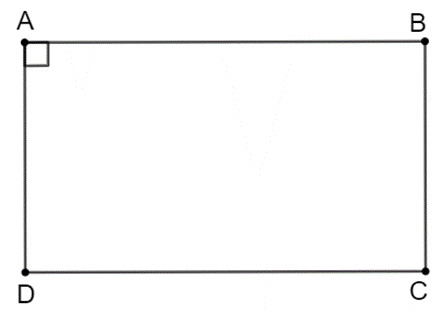
Vì ABCD là hình bình hành nên ˆA = ˆC; ˆB = ˆD.

Suy ra ˆC = ˆA = 90°.

Ta có ˆA + ˆB + ˆC + ˆD = 360°. 

90° + ˆB + 90° + ˆB = 360° => 2ˆB + 180° = 360°

Suy ra 2ˆB = 360° − 180° = 180°, do đó ˆB = 90°

Mà ˆB = ˆD nên ˆB = ˆD = 90o.

Hình bình hành ABCD có ˆA = ˆB = ˆC = ˆD = 90° => ABCD là hình chữ nhật.

Giải Toán 8 trang 66

Luyện tập 2: Cho tứ giác ABCD có Aˆ=90∘, hai đường chéo cắt nhau tạ trung điểm O của mỗi đường. Hỏi tứ giác ABCD là hình gì? Tại sao?

Lời giải

Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm O của mỗi đường 

=>  ABCD là hình bình hành.

Xét hình bình hành ABCD ta có:  Aˆ = 90∘ => ABCD là hình chữ nhật.