Giải Toán 8 Kết nối tri thức: Bài 12: Hình bình hành

Hướng dẫn Giải Toán 8 Kết nối tri thức Bài 12: Hình bình hành ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới

Giải Toán 8 trang 57

Hoạt động 1:

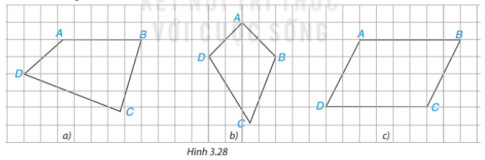
Trong hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?

Lời giải

Tứ giác trong Hình 3.28c là hình bình hành vì:

Ta so sánh độ dài các cạnh đối trong tứ giác bằng cách đếm số ô vuông trong hình và có các cặp cạnh song song

Ta thấy AB = CD; AD = BC.

Giải Toán 8 trang 58

Hoạt động 2:

Hãy nêu các tính chất của hình bình hành mà em biết

Lời giải

– Các cạnh đối song song;

– Các cạnh đối bằng nhau;

– Các góc đối bằng nhau;

– Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Hoạt động 3:

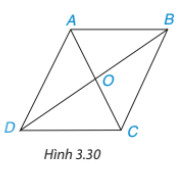
Cho hình bình hành ABCD (H.3.30)

a) Chứng minh ΔABC=ΔCDA. Từ đó suy ra AB = CD, AD = BC và ABCˆ=CDAˆ

b) Chứng minh ΔABD=ΔCDB. Từ đó suy ra DABˆ=BCDˆ

c) Gọi giao điểm của hai đường chéo AC, BD là O. Chứng minh ΔAOB=ΔCOD. Từ đó suy ra OA = OC, OB = OD

Lời giải

a) Xét tam giác ABC và CDA ta có:

BACˆ = DCAˆ (hai góc so le trong, AB // CD)

AC chung

ACBˆ = CABˆ (hai góc so le trong, AD // BC)

=>  ΔABC = ΔCDA (g.c.g)

Từ đó ta có: AB = CD, AD = BC và ABCˆ = CDAˆ

b) Xét tam giác ABD và CDB ta có:

ABDˆ = CDBˆ (hai góc so le trong, AB // DC)

BD chung

ADBˆ = CBDˆ (hai góc so le trong, AD // BC)

=> ΔABD = ΔCDB (g.c.g)

Từ đó ta có: DABˆ=BCDˆ

c) Xét tam giác AOB và COD ta có:

OABˆ = OCDˆ (hai góc so le trong, AB // DC)

AB = CD (cmt)

OBAˆ = ODCˆ (hai góc so le trong, AB // DC)

=> ΔAOB = ΔCOD (g.c.g)

Từ đó ta có: OA = OC, OB = OD

Luyện tập 1: 

Cho tam giác ABC. Từ một điểm M tùy ý trên cạnh BC, kẻ đường thẳng song song với AB, cắt cạnh

AC tại N và kẻ đường thẳng song song với AC, cắt AB tại P. Gọi I là trung điểm của đoạn NP. Chứng minh rằng I

cũng là trung điểm của đoạn thẳng AM.

Lời giải

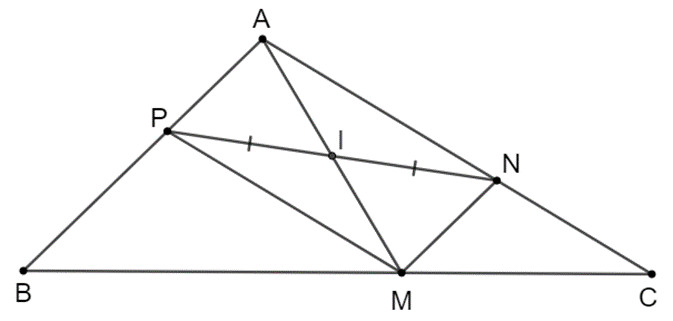
Xét tứ giác APMN có:

+ MN // AP (vì MN // AB)

+ MP // AN (vì MP // AC)

=> tứ giác APMN là hình bình hành.

Vậy hai đường chéo AM, NP cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của đoạn NP, nên I là trung điểm của đoạn thẳng AM.

Giải Toán 8 trang 60

Luyện tập 2: 

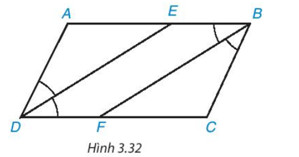
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E và tia phân giác của góc B cắt CD tại F (H.3.32)

a) Chứng minh hai tam giác ADE và CBF là những tam giác cân, bằng nhau

b) Tứ giác DEBF là hình gì? Tại sao?

Lời giải

a) Ta có: ADEˆ = EDCˆ (DE là phân giác góc D)

AEDˆ = EDCˆ (so le trong)

Suy ra AEDˆ = ADEˆ⇒ tam giác ADE là tam giác cân

Tương tự, ta chứng minh được tam giác CBF là tam giác cân

b) Xét tam giác ADE và CBF ta có:

AD = CB

Aˆ=Bˆ

AE = CF

Suy ra ΔADE = ΔCBF (c.g.c) ⇒DE=BF (1)

Ta có: EDFˆ = CBFˆ, CBFˆ = CFBˆ
⇒ EDFˆ = CFBˆ.(hai góc này ở vị trí đồng vị ) => DE // BF (2)

Từ (1) và (2) suy ra BEBF là hình bình hành

Giải Toán 8 trang 61

Luyện tập 3: 

Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi A', B' là các điểm sao cho O là trung

điểm của AA', BB'. Chứng minh rằng A'B' = AB và đường thẳng A'B' song song với đường thẳng AB.

Lời giải

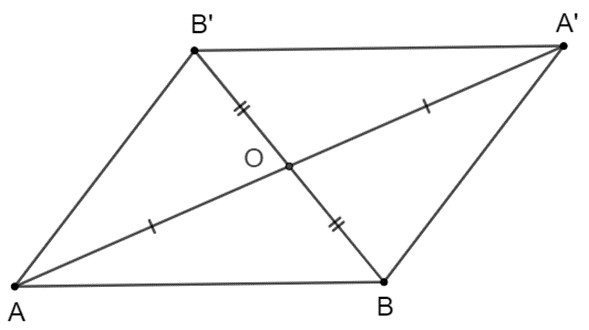
Ta có hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB.

 O là trung điểm của AA’, BB’ => O là trung điểm của hai đường chéo của tứ giác ABA’B’.

Do đó tứ giác ABA’B’ là hình bình hành.

Suy ra A’B’ = AB (định lí 1a) và A’B’ // AB (định nghĩa hình bình hành).