Bài 3.18 trang 61 SGK Toán 8 Tập 1 Kết nối tri thức

 Bài 12: Hình bình hành

Bài 3.18 trang 61 SGK Toán 8 Tập 1 Kết nối tri thức: Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh ΔOAM=ΔOCN. Từ đó suy ra tứ giác MBND là hình bình hành.

Lời giải:

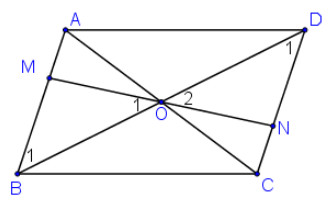
- Xét tam giác OAM và OCN ta có:

+ góc AOM = góc CON (đối đỉnh)

+ OA = ON

+ góc OAM = góc OCN (so le trong)

Suy ra ΔOAM = ΔOCN (g.c.g) 

do đó AM = CN

Lại có AB = CD, suy ra MB = ND

Như vậy: MB = ND, MB// ND ⇒ tứ giác MBND là hình bình hành

* Kiến thức vận dụng giải bài tập:

Chứng minh tứ giác MBND có:

+ BM // DN (vì AB // CD)

+ BM = DN

Do đó, tứ giác MBND là hình bình hành.