Giải Toán 8 Kết nối tri thức: Bài 11: Hình thang cân

Hướng dẫn Giải Toán 8 Kết nối tri thức Bài 11: Hình thang cân ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 8 trang 53

Luyện tập 1: 

Tính các góc của hình thang cân ABCD (AB // CD, biết Cˆ=40∘ (H.3.15)

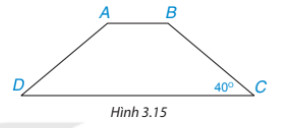
Lời giải

Hình thang cân ABCD (AB // CD) nên ta có:

ˆA = ˆB; ˆD = ˆC = 40°;

ˆA + ˆB + ˆC + ˆD = 360°.

Khi đó: 

ˆA + ˆA + 40° + 40° = 360° Hay 2ˆA + 80° = 360°

Suy ra 2ˆA = 360°− 80° = 280°.

Do đó ˆA = 140°nên ˆB = 140°.Vậy ˆA = 140°; ˆB = 40°; ˆC = 40°;ˆD = 40°.

Hoạt động 1: 

Cho hình thang cân ABCD, AB // CD và AB < CD (H.3.16).

a) Từ A và B kẻ AH⊥DC,BI⊥DC,H∈CD,I∈CD. Chứng minh rằng AH = BI bằng cách chứng minh ΔAHI=ΔIBA

b) Chứng minh ΔAHD = ΔBIC, từ đó suy ra AD = BC

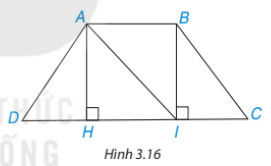
Lời giải

a) Vì ABCD là hình thang cân (AB // CD) nên ˆBAI = ˆAIH (hai góc so le trong).

Ta có AH ⊥ DC, BI ⊥ DC suy ra AH // BI.

Do đó ˆAIB = ˆHAI (hai góc so le trong).

Xét ∆AHI và ∆IBA có: ˆBAI=ˆAIH (chứng minh trên);

Cạnh AI chung;

ˆAIB = ˆHAI (hai góc so le trong).

Do đó ∆AHI = ∆IBA (c.g.c).

Suy ra AH = BI (hai cạnh tương ứng).

b) Vì ABCD là hình thang cân (AB // CD) nên ˆC=ˆD(1)

Xét ∆AHD vuông tại H có 

ˆDAH + ˆD = 90°(2) (trong tam giác vuông, hai góc nhọn có tổng số đo bằng 90°).

Tương tự, ∆BIC vuông tại I có ˆCBI + ˆC = 90°(3)

Từ (1), (2) và (3) suy ra ˆDAH = ˆCBI.

Xét ∆AHD và ∆BIC có: ˆAHD = ˆBIC=90° (vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);

AH = BI (chứng minh câu a);

ˆDAH = ˆCBI (chứng minh trên).

Do đó ∆AHD = ∆BIC (cạnh góc vuông – góc nhọn kề).

Suy ra AD = BC (hai cạnh tương ứng).

Luyện tập 2:

Cho tứ giác ABCD như Hình 3.18. Biết rằng ˆA = ˆB = ˆD1. Chứng minh rằng AD = BC.

Lời giải

Ta có ˆA = ˆD1 mà hai góc này ở vị trí đồng vị => AB // CD.

Suy ra tứ giác ABCD là hình thang.

Mặt khác hình thang ABCD có ˆA = ˆB nên ABCD là hình thang cân.

Do đó AD = BC (đpcm).

Giải Toán 8 trang 54

Hoạt động 2: 

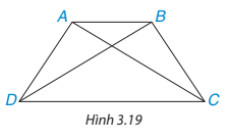
Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ΔACD = ΔBDC. Từ đó suy ra AC = BD.

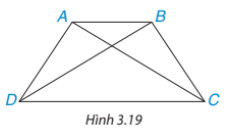
Lời giải

Vì ABCD là hình thang cân (AB // CD) => AD = BC; ˆADC = ˆBCD.

Xét ∆ACD và ∆BDC có:

AD = BC (chứng minh trên); 

ˆADC = ˆBCD (chứng minh trên);

Cạnh CD chung.

Vì vậy ∆ACD = ∆BDC (c.g.c).

Suy ra AC = BD (hai góc tương ứng).

Luyện tập 3: 

Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).

a) Tứ giác DECB là hình gì?

b) Chứng minh BE = CD

Lời giải

a) Theo đề bài: d // BC nên DE // BC => DECB là hình thang.

 Tam giác ABC cân tại A => ˆB = ˆC.

Hình thang DECB có ˆB = ˆC nên là hình thang cân.

b) Hình thang cân DECB có BE và CD là hai đường chéo.

Do đó BE = CD (đpcm).