Bài 3.8 trang 55 SGK Toán 8 Tập 1 Kết nối tri thức

Bài 11: Hình thang cân

Bài 3.8 trang 55 SGK Toán 8 Tập 1 Kết nối tri thức: Hình thang cân ABCD (AB // CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.

Lời giải:

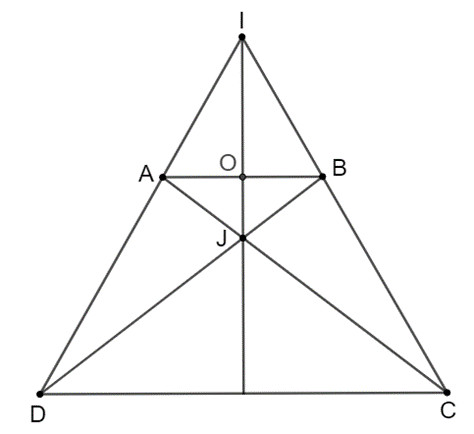
- Xét ∆ ACD và ∆ BDC có:

+ CD chung

+ AD = BC (tính chất hình thang)

+ AC = BD (do ABCD là hình thang cân)

=> ∆ACD = ∆BDC (c.c.c)

Suy ra  ACD = BDC hay góc JCD = góc JDC

⇒ Tam giác JCD cân tại I.

Do đó JD = JC (1)

Tam giác ICD có hai góc ở đáy bằng nhau

 góc C = góc D suy ra tam giác ICD cân tại I

⇒ ID = IC (2)

Từ (1) và (2) suy ra IJ là đường trung trực của CD.

Chứng minh tương tự có JA = JB, IA = IB

Suy ra J và I cùng thuộc đường trung trực của đoạn thẳng AB.

Do đó, IJ là đường trung trực của AB.

* Kiến thức vận dụng giải bài tập:

Gọi O là giao điểm của AB và IJ

Chứng minh: Tam giác IAB cân tại I (vì IA = IB) có IO là tia phân giác góc AIB

Suy ra IO là đường trung trực của đoạn thẳng AB.

Suy ra đường thẳng IJ là đường trung trực của đoạn thẳng AB