Bài 4.19 trang 74 SGK Toán 7 Tập 1 Kết nối tri thức

Luyện tập chung trang 74

Bài 4.19 trang 74 SGK Toán 7 Tập 1 Kết nối tri thức

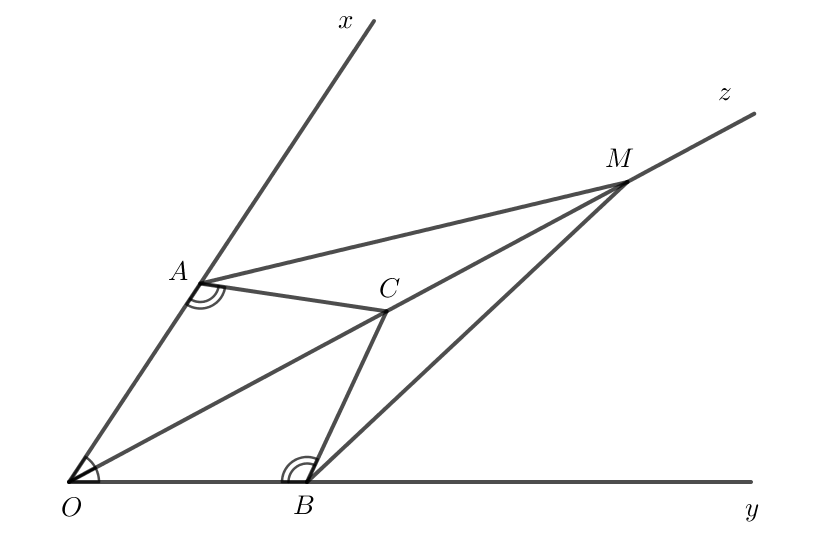
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho góc CAO = góc CBO

a) Chứng minh rằng ΔOAC = ΔOBC

b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng ΔMAC = ΔMBC

*Lời giải:
 

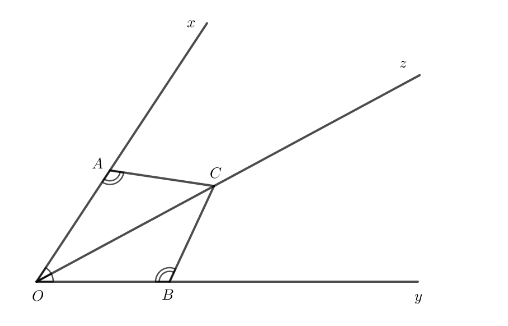
a)

Do Oz là tia phân giác của góc xOy nên góc AOC = góc BOC.

Trong tam giác ΔOAC có:

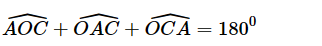
Trong tam giác ΔOBC có: 

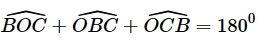
Mà góc AOC = góc BOC (do Oz là phân giác góc xOy) và góc CAO = góc CBO

Vậy góc OCA = góc OCB.

Xét hai tam giác ΔOAC và ΔOBC có

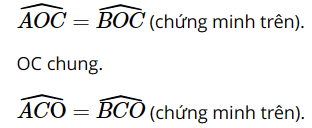
Vậy tam giác ΔOAC = ΔOBC (g-c-g)

b) 

Tam giác ΔOAC = ΔOBC

AO = BO

AC = BC

- Xét 2 tam giác ΔAOM và ΔBOM, ta có :

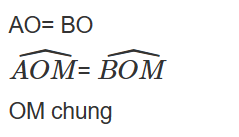
=> ΔAOM = ΔBOM (g-c-g)

Do đó: AM = BM

- Xét ΔMAC và ΔMBC , ta có :

AM = BM

MC chung

AC = BC

Vậy tam giác ΔMAC = ΔMBC (c-c-c)

*Kiến thức vận dụng giải bài tập

a) Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.

b) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – cạnh - cạnh.