Bài 2.25 trang 44 SGK Toán 8 Tập 1 Kết nối tri thức

Bài 9: Phân tích đa thức thành nhân tử

Bài 2.25 trang 44 SGK Toán 8 Tập 1 Kết nối tri thức:

Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2).

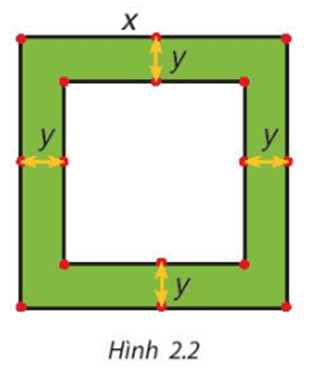
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.

b) Phân tích S thành nhân tử rồi tính S khi x = 102 m, y = 2 m.

Lời giải:

a) Giả sử đặt tên các điểm A, B, C, D, M, N, P, Q như hình vẽ dưới đây.

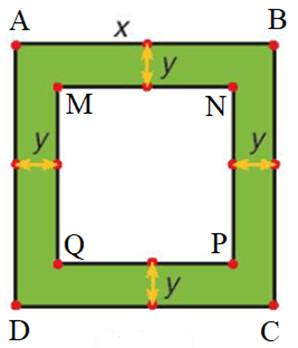
- Diện tích hình vuông ABCD là: x² (m).

- Hình vuông MNPQ có độ dài một cạnh là: x – y – y = x – 2y (m).

- Diện tích hình vuông MNPQ là: (x – 2y)² (m²).

- Diện tích S xung quanh mảnh vườn là:

S = x² – (x – 2y)² = x² – (x² – 4xy + 4y²)

= x² – x² + 4xy – 4y² = 4xy – 4y² (m²).

Vậy diện tích S của đường bao quanh mảnh vườn là 4xy – 4y² (m²).

b) Phân tích đa thức S thành nhân tử, ta có:

S = 4xy – 4y² = 4y(x – y).

Thay x = 102 m, y = 2 m vào biểu thức S, ta được:

S = 4 . 2 . (102 – 2) = 8 . 100 = 800 (m²).

* Kiến thức vận dụng giải bài tập:

Ta có biểu thức:

Diện tích đường bao quanh = diện tích mảnh vườn hình vuông – diện tích bên trong vườn.