Bài 10 trang 110 SGK Đại Số 10 nâng cao

Bài 1: Bất đẳng thức và chứng minh bất đẳng thức

Bài 10 (trang 110 SGK Đại Số 10 nâng cao)

Chứng minh rằng với hai số a, b, tùy ý, ta có:

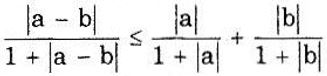
Đẳng thức xảy ra khi nào?

Lời giải:

(1) | a – b|(1 + |a| + |b| + |ab|) ≤ (|a| + |ab|)(1 + |a – b| + (|b| + |ab|)(1 + |a – b|)

⇔ |a – b| + |a(a – b)| + |b(a – b)| + |ab||a – b| ≤ |b(a – b)| + 2|ab| + 2|ab||a – b| + |a(a – b)| + |b(a – b)|

⇔ |a – b| ≤ |a| + |b| + 2|ab| + |ab(a – b)| (2)

Ta có : |a – b| = |a + (-b)| ≤ |a| + |-b| = |a| + |b|

Do vậy (2) đúng.

Dấu đẳng thức xảy ra ở (1) ⇔ dấu đẳng thức xảy ra ở (2)

⇔ |a – b| = |a| + |b| và 2|ab| + |ab( a – b)| = 0 ⇔ a = 0 hoặc b = 0

Tham khảo toàn bộ: Giải bài tập Toán 10 nâng cao