Điều kiện để hai đường thẳng cắt nhau

Với hai đường thẳng y = ax + b (d) và y = a'x + b' (d') ( trong đó a và a’ khác 0), ta có:

(d) và (d’) cắt nhau ⇔ a ≠ a'.

Để hiểu rõ hơn về điều kiện hai đường thẳng cắt nhau, mời các bạn cùng Toploigiai đến với phần nội dung dưới đây.

1. Hai đường thẳng cắt nhau là gì?

Hai đường thẳng chỉ có một điểm chung gọi là hai đường thẳng cắt nhau và điểm chung được gọi là giao điểm của hai đường đó.

Với hai đường thẳng y = ax + b (d) và y = a'x + b' ( trong đó a và a’ khác 0), ta có:

Điều kiện để (d) và (d’) cắt nhau ⇔ a ≠ a'.

>>> Tham khảo: Cách tìm tọa độ giao điểm của hai đường thẳng

2. Các dạng toán thường gặp hai đường thẳng cắt nhau

Như vậy, với từng dạng toán về hai đường thẳng cắt nhau ta có cách giải khác nhau. 

Dạng 1: Chứng minh hai đường thẳng đã cho cắt nhau. Phương pháp làm như sau:

Bước 1: Lập hệ phương trình giao điểm của của hai đường thẳng

Bước 2: Tìm nghiệm của hệ phương trình đó. Nếu hệ phương trình có nghiệm chứng tỏ hai đường thẳng cắt nhau. Nếu hệ phương trình vô nghiệm thì hai đường thẳng không cắt nhau. Nếu hệ phương trình vô số nghiệm thì hai đường thẳng đó trùng nhau.

Bước 3: Kết luận và kiểm tra lại bài.

Đây là phương pháp chung đối với dạng toán này. Nếu mà hai phương trình đường thẳng đã cho là hai đường thẳng cụ thể thì có thể tìm trực tiếp nghiệm. Nếu hai đường thẳng cho ở dạng tham số thì cần biện luận theo tham số. Trong nhiều trường hợp kể cả là phương trình chứa tham số nhưng vẫn tìm được giao điểm cụ thể của hai đường thẳng.

Dạng 2: Chứng minh một điểm thuộc đường thẳng này cũng thuộc đường thẳng kia. 

Đây là dạng toán cơ bản mà tất cả học sinh đều được làm. Nó sẽ giúp học sinh hiểu rõ hơn mối quan hệ cắt nhau giữa hai đường thẳng.

Phương pháp làm hết sức đơn giản. Chỉ cần thay giá trị tọa độ của điểm đã cho vào công thức hai đường thẳng. Nếu cả hai đều thỏa mãn (luôn đúng) thì chứng minh được bài toán. Điều này cũng có nghĩa là đây chính là giao điểm của hai đường thẳng.

>>> Tham khảo: Hai đường thẳng cắt nhau tạo ra hai góc đối đỉnh thì?

3. Bài tập luyện tập

Bài 1: Cho hai hàm số y = mx + 3 và y =(2m - 1)x - 5

Tìm giá trị của m để đồ thị của hai hàm số đã cho là:

Hai đường thẳng cắt nhau.

Lời giải

Đồ thị của hai hàm số đã cho là hai đường thẳng cắt nhau khi và chỉ khi:

Vậy với m ≠ 0; m ≠ 1/2; m ≠ 1 là các giá trị cần tìm

Bài 2: Cho hàm số y = (2m - 3)x + m - 5. Tìm m để đồ thị hàm số:

a, Tạo với 2 trục tọa độ một tam giác vuông cân

b, Cắt đường thẳng y = 3x - 4 tại một điểm trên Oy

c, Cắt đường thẳng y = -x - 3 tại một điểm trên Ox

Lời giải:

Để hàm số là hàm số bậc nhất ⇔ 2m−3 ≠ 0 ⇔ m ≠ 3/2

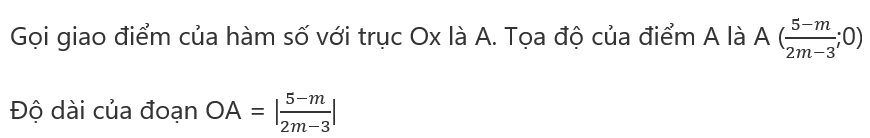
Gọi giao điểm của hàm số với trục Oy là B. Tọa độ của điểm B là B (0; m−5)

Độ dài của đoạn OB = |m−5| 

Ta có tam giác OAB là tam giác vuông tại A

Vậy với m = 1 hoặc m = 2 thì đồ thị hàm số tạo với hai trục tọa độ tam giác vuông cân

b, Gọi A là điểm đồ thị hàm số cắt đường thẳng y = 3x - 4 tại một điểm trên trục Oy (trục tung) ⇒ A (0; b)

Thay tọa độ điểm A vào đồ thị hàm số y = 3x - 4 ta có b = 4

Điểm A (0; 4) thuộc đồ thị hàm số y = (2m - 3)x + m - 5 nên ta có

4 = (2m−3).0+m−5 ⇔ m−5 = 4 ⇔ m=9 (tm) 

Vậy với m = 9 thì đồ thị hàm số cắt đường thẳng y = 3x - 4 tại một điểm trên trục tung

c, Gọi B là điểm đồ thị hàm số cắt đường thẳng y = - x - 3 tại một điểm trên trục Ox (trục hoành) ⇒ B (a; 0)

Thay tọa độ điểm B vào đồ thị hàm số y = - x - 3 ta có a = - 3

Điểm B (-3; 0) thuộc đồ thị hàm số y = -x - 3 nên ta có:

0 = (−3)(2m−3)+m−5 ⇔ −5m+4=0 ⇔ m = 4/5 (tm)

Vậy với m = 4/5 thì đồ thị hàm số cắt đường thẳng y = -x - 3 tại một điểm trên trục hoành

Bài 3: Với giá trị nào của m thì đồ thị các hàm số y = 3x + 1 - m và y = -2x + m + 3 cắt nhau tại một điểm:

a, Trên trục tung

b, Trên trục hoành

Lời giải

a, Đồ thị hàm số y = 3x + 1 - m cắt trục tung tại A(0; 1 - m). Nên đồ thị của hai hàm số trên cắt nhau tại một điểm trên trục tung thì điểm đó phải là A(0; 1 - m)

Đồ thị hàm số y = -2x + m + 3 đi qua A(0; 1 - m) <=> 1 - m = 2.0 + m + 3 <=> m = -1

-------------------------------

Trên đây, Toploigiai đã cùng các bạn tìm hiểu về điều kiện để hai đường thẳng cắt nhau. Chúng tôi hi vọng bài viết này giúp ích cho các bạn, chúc các bạn học tốt.