Bài 9: Các số đặc trưng đo xu thế trung tâm
Hướng dẫn Giải Toán 11 Kết nối tri thức Bài 9: Các số đặc trưng đo xu thế trung tâm ngắn gọn kèm lời giải và đáp
án chi tiết bám sát nội dung chương trình Sách mới.
Giải Toán 11 trang 62
Hoạt động 1: Khảo sát thời gian tự học của các học sinh trong lớp theo mẫu bên
a) Hãy lập bảng thống kê cho mẫu số liệu ghép nhóm thu được
b) Có thể tính chính xác thời gian tự học trung bình của các học sinh trong lớp
không?
c) Có cách nào tính gần đúng thời gian tự học trung bình của các học sinh trong lớp
dựa trên mẫu số liệu ghép nhóm này không?
Lời giải:
a) Giả sử lớp 11A có 30 học sinh và sau khi khảo sát, ta có được bảng thống kê như sau
| Số giờ tự học (giờ) | [0; 1,5) | [1,5; 3) | [3; 4,5) | ≥ 4,5 |
|---|---|---|---|---|
| Số học | 8 | 23 | 6 | 3 |
b) Không thể tính chính xác thời gian tự học trung bình của các học sinh trong lớp vì không có mẫu số liệu cụ
thể về thời gian tự học của từng học sinh, chúng ta chỉ có thể tính số gần đúng thời gian tự học trung bình của các
học sinh trong lớp.
c) Giá trị đại diện của nhóm bằng trung bình giá trị đầu mút phải và trái của nhóm đó.
Nhóm ≥ 4,5 là nhóm mở nên ta dựa theo nhóm gần đó nhất là nhóm [3; 4,5) để lấy giá trị đại diện.
| Số giờ tự học (giờ) | [0; 1,5) | [1,5; 3) | [3; 4,5) | ≥ 4,5 |
|---|---|---|---|---|
| Giá trị đại diện | 0,75 | 2,25 | 3,75 | 5,25 |
Giá trị trung bình của mẫu số liệu trên là : 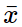 = (0,75 . 8 + 2,25 .23 + 3,75 . 6 + 5,25 . 3)/30 = 3,2
= (0,75 . 8 + 2,25 .23 + 3,75 . 6 + 5,25 . 3)/30 = 3,2
Giải Toán 11 trang 63
Luyện tập 1: Tìm hiểu thời gian xem ti vi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả như sau:

Tính thời gian xem ti vi trung bình trong tuần trước của các bạn học sinh .
Lời giải:
| Thời gian học ( giờ) | [0; 5) | [5; 10) | [10; 15) | [15; 20) | [20; 25) |
|---|---|---|---|---|---|
| Số học sinh | 8 | 16 | 4 | 2 | 22 |
| Giá trị đại diện | 2,5 | 7,5 | 12,5 | 17,5 | 22,5 |
Tổng số học sinh của lớp là: 8 + 16 + 4 + 2 + 2 = 32
Thời gian xem ti vi trung bình trong tuần trước của các bạn học sinh này là:
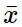 = (8.2,5 + 16.7,5 + 4.12,5 + 2 .17,5 + 2.22,5) / 32 = 8.4375 (giờ)
= (8.2,5 + 16.7,5 + 4.12,5 + 2 .17,5 + 2.22,5) / 32 = 8.4375 (giờ)
Hoạt động 2: Cho mẫu số liệu ghép nhóm về chiều cao của 21 cây na giống

Gọi x1,x2,...,x21 là chiều cao của các cây giống, đã được sắp xếp theo thứ tự tăng dần. Khi đó, x1,...,x3 thuộc [0;5),
x4;...;x11 thuộc [5;10),... Hỏi trung vị thuộc nhóm nào?
Lời giải:
Cỡ mẫu n = 3 + 8 + 7 + 3 = 21
Suy ra trung vị là x11 thuộc nhóm [5;10)
Giải Toán 11 trang 64
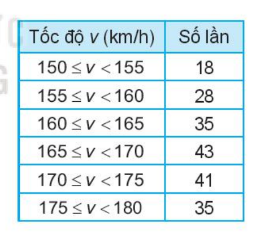
Luyện tập 2: Ghi lại tốc độ bóng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết quả như bảng bên. Tính trung vị của mẫu số liệu ghép nhóm này
Lời giải:
Cỡ mẫu là: n = 18 + 28 + 35 + 43 + 43 + 41 + 35 = 200
Gọi x1, x2... x200 là tốc độ giao bóng của 200 lần và giả sử dãy này được sắp xếp theo thứ tự tăng dần.
Khi đó trung vị là (x100 + x101 )/2
Hai giá trị x100, x101 thuộc nhóm [165; 170) nên nhóm này chứa trung vị.
=> p = 4;
a4 = 165;
m4 = 43;
m1 + m2 + m3 = 18 + 28 + 35 = 81;
a5 − a4 = 5
=> Me = 165 + (200/2 − 81)/43 . 5 = ,21
Hoạt động 3: Với mẫu số liệu ghép nhóm cho trong HĐ2, hãy cho biết tứ phân vị thứ nhất Q1 và tứ phân vị thứ ba
Q3 thuộc nhóm nào.

Lời giải:
Cỡ mẫu là: n = 21
Tứ phân vị thứ nhất Q1 là (x5 + x6)/2. Do x5; x6 đều thuộc nhóm [5; 10) nên tứ phân vị thứ nhất thuộc nhóm [5; 10)
Tứ phân vị thứ ba Q3 là (x16 + x17)/2. Do x16, x17 đều thuộc nhóm [10; 15) nên tứ phân vị thứ ba thuộc nhóm
[10; 15)
Giải Toán 11 trang 65
Luyện tập 3: Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba cho mẫu số liệu ghép nhóm ở Luyện tập 2
Lời giải:
Cỡ mẫu: n = 200
Tứ phân vị thứ nhất Q1 là (x50 + x51)/2. Do x50; x51 đều thuộc nhóm [160; 165) nên tứ phân vị thứ nhất thuộc nhóm [160; 165).
Do đó, p = 3; a3 = 160; m3 = 35; m1 + m2 = 18 + 28 = 46; a4 − a3 = 5 và ta có:
Q1 = 160 + (200/4 − 46)/35 . 5 = 160,57
Tứ phân vị thứ ba Q3 là (x150 + x151)/ 2. Do x150,x151 đều thuộc nhóm [170;175) nên tứ phân vị thứ ba thuộc nhóm
[170;175).
Do đó, p = 5; a5 = 170; m5 = 41; m1 + m2 + m3 + m4 = 18 + 28 + 35 + 43 = 124; a6 − a5 = 5 và ta có:
Q3 = 170 + (600/4 − 124)/41 . 5 = 173,17
Giải Toán 11 trang 66
Hoạt động 4: Với số liệu cho trong Luyện tập 1:
a) Có thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh không?
b) Mốt thuộc nhóm nào là hợp lí nhất? Nên lấy số nào trong nhóm để ước lượng cho mốt?
Lời giải:
a) Không thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh
b) Tần số lớn nhất là 16 nên nhóm chứa mốt là [5; 10)
Ta có j = 2, a2 = 5, m2 = 16, m1 = 8; m3 = 4, h = 5. Do đó:
Mo = 5 + 16 − 8/[(16 − 8) + (16 − 4)] . 5 = 7
Luyện tập 3: Thời gian (phút) để học sinh hoàn thành một câu hỏi thi được cho như sau:

Tìm mốt của mẫu số liệu ghép nhóm này
Lời giải:
Tân số lớn nhất là 10 nên nhóm chứa mốt là nhóm [10.5; 20.5] .
Ta có, j = 2; a2 = 10,5; m2 = 10; m1=2 ; m3 = 6; h = 10.
Do đó:
Mo = 10,5 + (10 − 2)/[(10 − 2) + (10 − 6)] .10 = 17,17
Vận dụng: Hãy tính các số đặc trưng cho mẫu số liệu trong Bảng 3.1 và giải thích ý nghĩa của các giá trị thu được.
Lời giải:
| Số tiền ( nghìn đồng) | [0; 30) | [30; 60) | [60; 90) | [90; 120) |
|---|---|---|---|---|
| Số khách | 3 | 15 | 10 | 7 |
| Giá trị đại diện | 15 | 45 | 75 | 105 |
Cỡ mẫu là: n = 3 + 15 + 10 + 7 = 35
Số trung bình là: 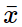 = (3.15 + 15.45 + 10.75 + 7.105)/(3 + 15 + 10 + 7) = 63
= (3.15 + 15.45 + 10.75 + 7.105)/(3 + 15 + 10 + 7) = 63
Giải thích: Xấp xỉ bằng số trung bình của mẫu số liệu gốc cho biết vị trí trung tâm của mẫu số liệu và đại diện cho mẫu số liệu
Trung vị là x18 thuộc nhóm [30;60), do đó p = 2; a2 = 30; m2 = 15; m1 = 3; a3 − a2= 30 và ta có:
Me = 30 + (35/2 − 3)/15 . 30 = 59
Giải thích: Xấp xỉ bằng trung vị của mẫu số liệu gốc, chia mẫu số liệu thành 2 phần, mỗi phần chứa 50% giá trị
Tứ phân vị thứ nhất Q1 là x9 thuộc nhóm [30; 60), do đó p = 2; a2 = 30; m2 = 15; m1 = 3; a3 − a2 = 30 và ta có:
Q1 = 30 + (35/4 − 3)/15 . 30 = 41.5
Giải thích: Có 25% số giá trị nhỏ hơn 41.5
Tứ phân vị thứ ba Q3 là x27 thuộc nhóm [60; 90), do đó p = 3; a3 = 60; m3 = 10; m1 + m2 = 3 + 15 = 18; a4 − a3 = 30 và ta có:
Q3 = 30 + (3 . 35/4 − 18)/10 . 30 = 54,75
Giải thích: Có 75% số giá trị nhỏ hơn 54.75%
Tần số lớn nhất là 15 nên mốt thuộc nhóm [30; 60). Ta có, j = 2;a2 = 30; m2 = 15; m1 = 3; m3 = 10; h = 30, do đó:
Mo = 30 + (15 − 3)/[(15 − 3) + (15−10)] . 30 = 51,18
Giải thích: Xấp xỉ bằng mốt của mẫu số liệu gốc, được dùng để đo xu thế trung tâm của mẫu số liệu

