Bài 4.17 trang 88 SGK Toán 8 Tập 1 Kết nối tri thức

Luyện tập chung trang 88

Bài 4.17 trang 88 SGK Toán 8 Tập 1 Kết nối tri thức: Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: DM²=MN×MK

Lời giải:

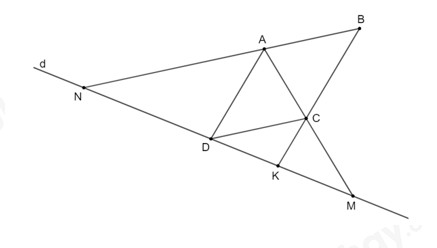
Vì ABCD là hình bình hành nên AB // CD, AD // BC 

suy ra =>  AN // CD, AD // CK.

Áp dụng định lí Thales vào tam giác AMN ta có:

AN // CD => DM/MN = CM/AM       (1) 

Áp dụng định lí Thales vào tam giác ADM ta có:

CK // AD => MK/DM = CM/AM      (2)

Từ (1) và (2) suy ra: DM/MN = MK/DM = CM/AM

Như vậy DM² = MN . MK (đpcm).

* Kiến thức vận dụng giải bài tập:

Áp dụng định lí Thales cho AN // CD, CK // AD, ta có lần lượt các tỉ lệ thức DM/MN = CM/AM và MK/DM = CM/AM. Từ đó ta suy ra đpcm.