Bài 4.14 trang 88 SGK Toán 8 Tập 1 Kết nối tri thức

Luyện tập chung trang 88

Bài 4.14 trang 88 SGK Toán 8 Tập 1 Kết nối tri thức: 

Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC

a) Chứng minh EF // CD, FK // AB

b) So sánh EF và 1/2(AB+CD)

Lời giải:

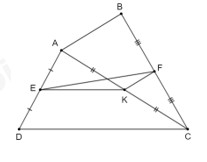
a) Xét ΔADC ta có:

+ E là trung điểm của AD

+ K là trung điểm của AC

=> EK là đường trung bình của ΔADC

Suy ra: EK//DC

Xét ΔABC ta có:

+ K là trung điểm của AC

+ F là trung điểm của BC

=> KF là đường trung bình của ΔABC

Suy ra: KF//AB

b) EK là đường trung bình của ΔADC => EK = CD/2

KF là đường trung bình của ΔABC => KF = AB/2

Ta có: EF ≤ EK + KF = CD/2 + AB/2 = (AB+CD)/2

* Kiến thức vận dụng giải bài tập:

a. Chứng minh EK là đường trung bình của tam giác => FK // AB.

b. Vận dụng tính chất đường trung bình với EK và Fk trong tam giác ACD, ABC. 

Sau đó áp dụng bất đẳng thức tam giác KEF, suy ra đpcm.