Bài 17: Hàm số liên tục

Hướng dẫn Giải Toán 11 Kết nối tri thức Bài 17: Hàm số liên tục ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 11 trang 119

Hoạt động 1: Nhận biết tính liên tục của hàm số tại một điểm

Cho hàm số:

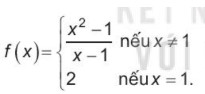
Tính giới hạn 

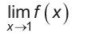
và so sánh giá trị này với f(1)

Lời giải:

Ta có:

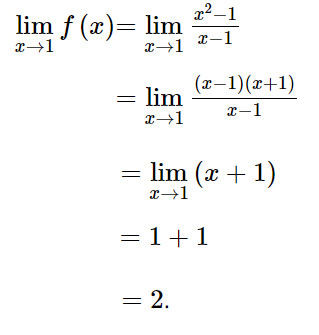
Mà f(1) = 2 nên

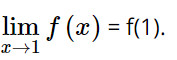
Giải Toán 11 trang 120

Luyện tập 1:  Xét tính liên tục của hàm số

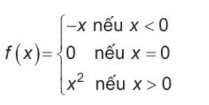
tại điểm x₀ = 0

Lời giải:

Tập xác định của hàm số f(x) là D = R

Ta có:

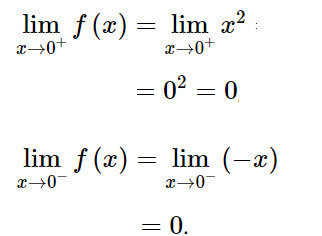
Khi đó

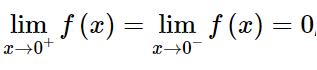
Vì vậy:

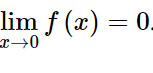
Mà f(0) = 0 nên:

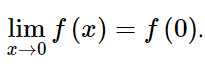
Vậy hàm số f(x) liên tục tại 0. 

Hoạt động 2: Cho hai hàm số 

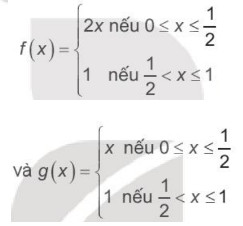
 với đồ thị tương ứng như Hình 5.7

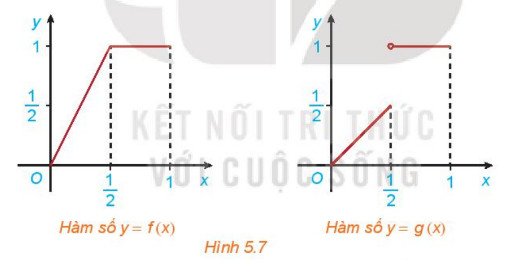
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm x = 1/2 và nhận xét sự khác nhau giữa hai đồ thị

Lời giải:

+) Điểm x = 1/2 thuộc tập xác định của hàm số f(x) nên ta có:

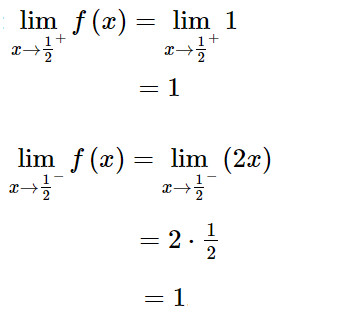
Khi đó:

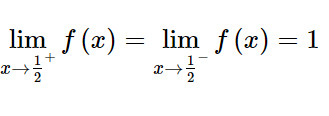
Do đó:

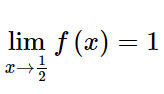
Ta có f(1/2) = 1 nên 

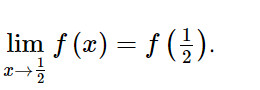
Vậy hàm số f(x) liên tục tại điểm x = 1/2

+) Điểm x = 1/2 thuộc tập xác định của hàm số g(x) nên ta có:

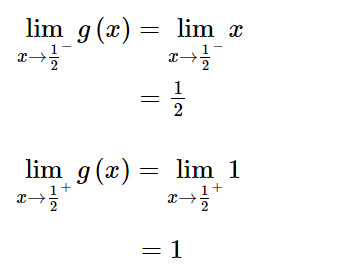
Ta thấy:

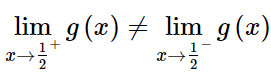
Vậy hàm số g(x) không liên tục mà bị gián đoạn tại điểm x = 1/2

+) Nhận xét:

Đồ thị hàm số f(x) là các đoạn thẳng nối liền nhau

Đồ thị hàm số g(x) là các đoạn thẳng rời nhau

Giải Toán 11 trang 121

Luyện tập 2: Tìm các khoảng trên đó hàm số f(x) = x² + 1/x + 2 liên tục

Lời giải:

Hàm số f(x) = (x² + 1)/(x + 2) có nghĩa khi x + 2 ≠ 0 hay x ≠ – 2.

Tập xác định của f(x) là (−∞;−2)∪(−2;+∞).

Vậy tại các khoảng (−∞;−2) và (−2;+∞) thì hàm số f(x) liên tục.

Hoạt động 3: Cho hai hàm số f(x) = x² và g(x) = - x + 1

a) Xét tính liên tục của hai hàm số trên tại x = 1

b) Tính

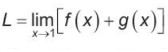
và so sánh L với f(1) + g(1)

Lời giải:

a) Ta có:

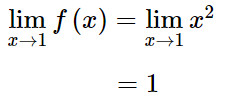
Mà f(1) = 1 do đó hàm số f(x) liên tục tại 1.

Ta có:

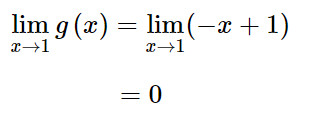
Mà g(1) = 0 do đó hàm số g(x) liên tục tại 1.

b) Ta có:

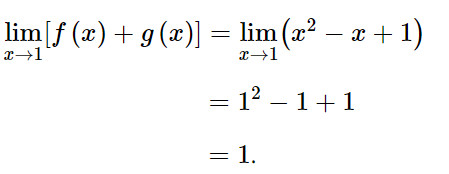
Mà  f(1) = 1² = 1; g(1) = – 1 + 1 = 0 =>  f(1) + g(1) = 1 + 0 = 1.

Vậy L = f(1) + g(1) = 1

Giải Toán 11 trang 122

Vận dụng: Giải bài toán ở tình huống mở đầu

Lời giải:

Theo bài ra ta có, vận tốc trung bình của xe trên quãng đường đó là:

v = s/t = 180/3 = 60 (km/h)

Gọi vận tốc của xe tại thời điểm t là v(t) ta có:

Vận tốc ban đầu của xe tại thời điểm t₀ là  v(t₀) = 0 

Vậy tại một thời điểm t₁ thì xe chạy với vận tốc v(t₁) > v_a.

Xét  f(t) = v(t) – v_a, ta nhận thấy f(t) liên tục trên đoạn [t₀; t₁].

Mà f(t₀) = – v_a < 0 và f(t₁) = v(t₁) – v_a > 0 (do v(t₁) > v_a)

=> Tồn tại thời điểm t* thuộc khoảng (t₀; t₁) sao cho f(t*) = 0. 

Khi đó ta có v(t*) – v_a = 0 hay v(t*) = v_a = 60.

Vậy sẽ tồn tại ít nhất một thời điểm xe chạy với vận tốc 60 km/h.