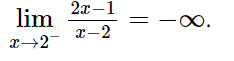Bài 16: Giới hạn của hàm số

Hướng dẫn Giải Toán 11 Kết nối tri thức Bài 16: Giới hạn của hàm số ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 11 trang 111

Hoạt động 1: Nhận biết khái niệm giới hạn tại một điểm

Cho hàm số f(x) = 4 − x²/x − 2

a) Tìm tập xác định của hàm số f(x)

b) Cho dãy số x_n = (2n + 1)/n. Rút gọn f(x_n) và tính giới hạn của dãy (u_n) với u_n = f(x_n)

c) Với dãy số (x_n) bất kì sao cho x_n ≠ 2 và x_n −> 2, tính f(x_n) 

và tìm :

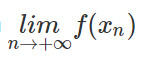
Lời giải:

a) Tập xác định của hàm số D:

Biểu thức f(x) có nghĩa khi x – 2 ≠ 0 <=> x ≠ 2.

Vậy  D = R \ {2}.

b) 

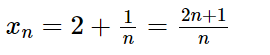
Ta có:

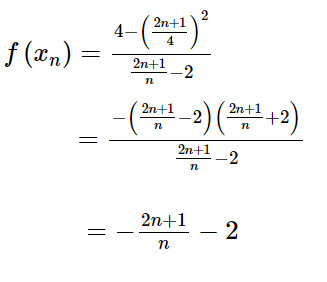
Vậy:

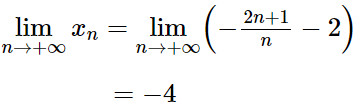
c) Ta có:

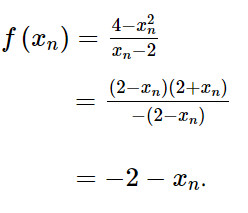
Vì x_n ≠ 2 và x_n −> 2 với mọi n nên

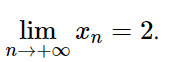
Vậy:

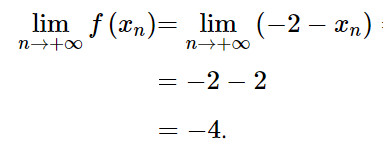
Giải Toán 11 trang 113

Luyện tập 1: Tính:

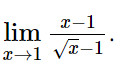
Lời giải:

Ta có:

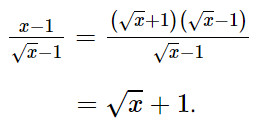
Nên:

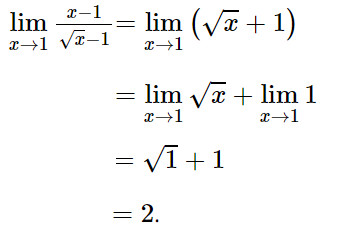
Vậy:

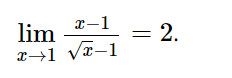
Hoạt động 2: Nhận biết khái niệm giới hạn một bên

Cho hàm số f(x) = |x − 1|/x − 1

a) Cho x_n = n/n + 1 và x′_n=n + 1/n. Tính y_n = f(x_n) và y′_n = f(x′_n)

b) Tìm giới hạn của các dãy số (y_n) và (y′_n)

c) Cho các dãy số (x_n) và (x′_n) bất kì sao cho x_n < 1 < x′_n và x_n −−>1, x′_n −−> 1, tính

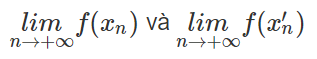
Lời giải:

a) Với x_n= n /(n + 1) ta có:

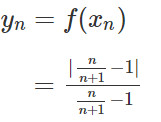
 n < n + 1   => n /n + 1 < 0  => n /n + 1 − 1 < 0 nên:

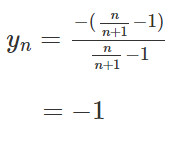
Với x′_n = (n + 1)/n ta có:

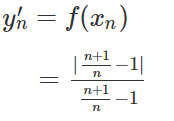
Vì n + 1 > n => (n + 1)/n > 1 => (n + 1)/n − 1 > 0 nên:

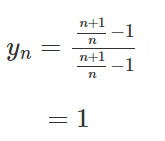
Luyện tập 2: Cho hàm số f(x):

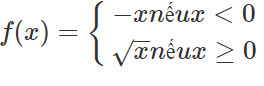
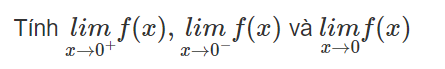
Lời giải:

Với dãy số (x_n) bất kì sao cho x_n < 0 và x_n −> 0:

Ta có f(x_n) = – x_n.

Do đó

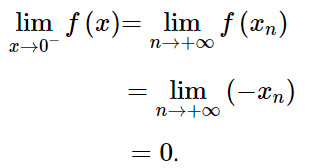
Tương tự như trên, với dãy số (x_n) bất kì sao cho x_n < 0 và x_n −> 0:

Ta có ta có f(x_n) = √x_n.

Do đó:

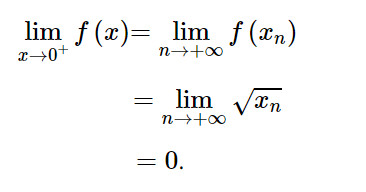
Vì:

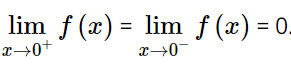
Nên 

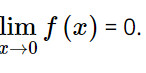
Giải Toán 11 trang 114

Hoạt động 3: Nhận biết khái niệm giới hạn tại vô cực

Cho hàm số f(x)=1 +  2/x−1 có đồ thị như Hình 5.4

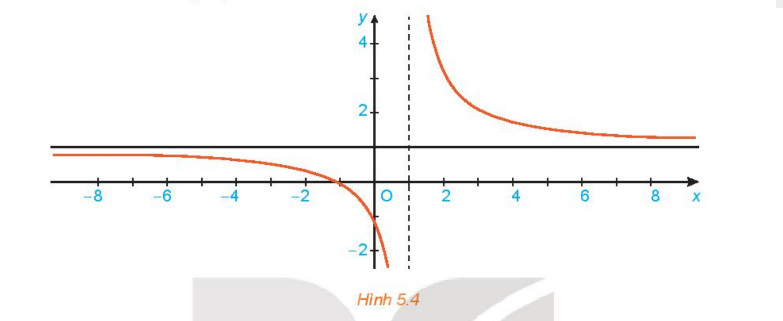
Giả sử (x_n) là dãy số sao cho x_n > 1, x_n −> +∞. Tính f(x_n) và tìm

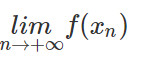
Lời giải:

Giả sử (x_n) là dãy số sao cho x_n > 1, x_n −> +∞.

Ta có:

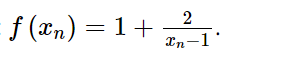
và khi n dần tới +∞ thì:

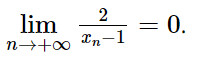
Do đó:

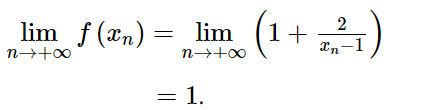
Giải Toán 11 trang 115 

Luyện tập 3: Tính

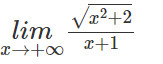
Lời giải:

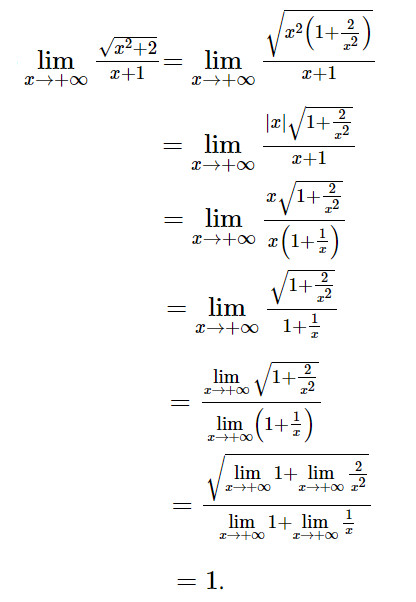
Vận dụng: Cho tam giác vuông OAB với A = (a;0) và B = (0;1) như Hình 5.5. Đường cao OH có độ dài là h

a) Tính h theo a

b) Khi điểm A dịch chuyển về O, điểm H thay đổi thế nào? Tại sao?

c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, điểm H thay đổi thế nào? Tại sao?

Lời giải:

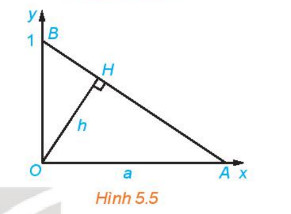
a) Tam giác vuông OAB có đường cao OH nên ta có:

1/OH² = 1/OA² + 1/OB²

Với A = (a; 0) => OA = a; B = (0; 1) => OB = 1; OH = h;

Ta có:

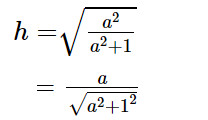
b)

Khi A dịch chuyển về O thì điểm H dịch chuyển về gần A hơn vì: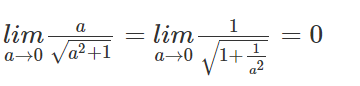

c) 

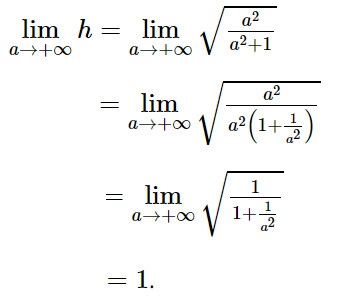
Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, điểm H dịch chuyển về phía điểm B, và h dần về .

Hoạt động 4: Nhận biết khái niệm giới hạn vô cực

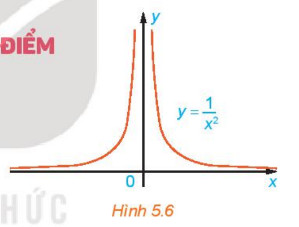
Xét hàm số f(x) = 1/x² có đồ thị như Hình 5.6

Cho x_n = 1/n, chứng tỏ rằng f(x_n) −> +∞.

Lời giải :

Tập xác định của hàm số f(x) là:  D = R \{0} 

x_n = 1/n vậy f(x_n) = 1/x_n²            

                                     = 1/(1/n)²

                                     = n²

Ta có:

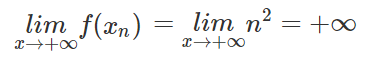
Vậy  f(xn) −> +∞.

Giải Toán 11 trang 116

Hoạt động 5: Cho hàm số f(x) = 1/x−1. Với các dãy số (x_n) và (x′_n) cho bởi x_n = 1 + 1/n, x′_n = 1 − 1/n, tính

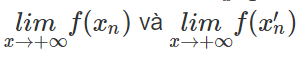
Lời giải:

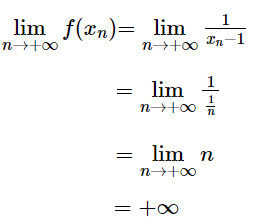
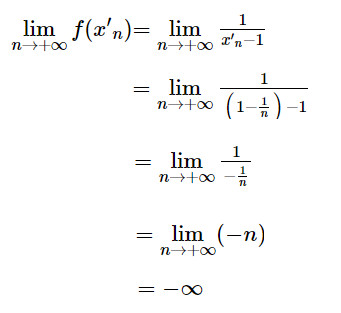
Luyện tập 4: Tính các giới hạn

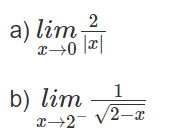
Lời giải:

a) Với dãy số (x_n) bất kì sao cho x_n ≠ 0, x_n −> 0.

Ta có:

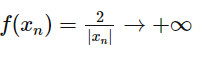
Do đó:

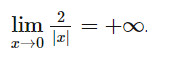
b)  Đặt g(x) = 1/(√2 − x ) Với mọi dãy số (x_n) trong khoảng (– ∞; 2) mà tại đó:

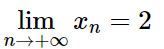
Khi đó:

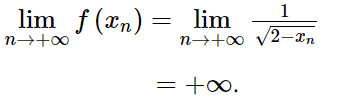
Vậy :

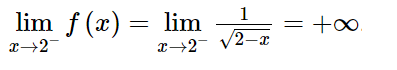
Giải Toán 11 trang 118

Luyện tập 5: Tính

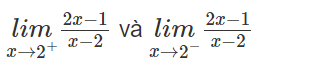
Lời giải:

- Ta có:

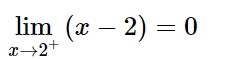
x − 2 > 0 với mọi x > 2. 

Do đó:

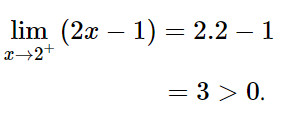
Vậy :

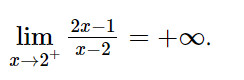
- Ta có:

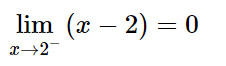
x – 2 < 0 với mọi x < 2.

Do đó:

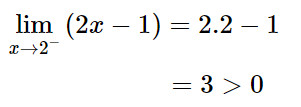
Vậy: