Bài 11: Hai đường thẳng song song

Hướng dẫn Giải Toán 11 Kết nối tri thức Bài 11: Hai đường thẳng song song ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 11 trang 78

Hoạt động 1: Quan sát bốn tuyến đường trong Hình 4.13 và trả lời các câu hỏi sau:

a) Hai tuyến đường nào giao nhau

b) Hai tuyến đường nào không giao nhau

c) Hai tuyến đường nào song song?

Lời giải:

a) Hai tuyến đường giao nhau: Tuyến màu cam và màu xanh dương, tuyến màu cam và màu đỏ

b) Hai tuyến đường không giao nhau:  tuyến màu xanh lá và tuyến màu xanh dương, tuyến màu xanh lá và tuyến

màu đỏ, tuyến màu xanh lá và tuyến màu cam, tuyến màu xanh dương và tuyến màu đỏ

c) Hai tuyến đường song song: Tuyến màu xanh dương và tuyến màu đỏ, tuyến màu xanh lá là tuyến màu cam

Giải Toán 11 trang 79

Câu hỏi: Hãy tìm một số hình ảnh về hai đường thẳng song song, hai đường thẳng chéo nhau trong thực tiễn.

Lời giải:

 Hai đường thẳng song song: hai mép bàn, đường cao tốc,...

Hai đường thẳng chéo nhau: kim tư tháp Ai Cập,...

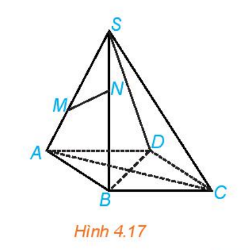
Luyện tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.17)

a) Trong các đường thẳng AB, AC, CD, hai đường thẳng nào song song, hai đường thẳng nào cắt nhau?

b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh SA, SB. Trong các đường thẳng nào chéo nhau hay không?

Lời giải:

a) 

Hai đường thẳng cắt nhau: AB và AC, AC và CD

Hai đường thẳng song song: AB và CD

b)

 M  thuộc SA và N thuộc SB => M và N thuộc mp(SAB)

Các đường thẳng SA, AF, MN cùng nằm trên mặt phẳng (SAB) nên chúng không chéo nhau

Giải Toán 11 trang 80

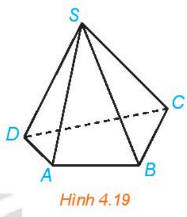
Luyện tập 2: Trong hình chóp tứ giác S. ABCD (H. 4.19), chỉ ra những đường thẳng:

a) Chéo với đường thẳng SA

b) Chéo với đường thẳng BC

Lời giải:

a) Đường thẳng chéo với SA: CD, CB.

b) Đường thẳng chéo với BC: SA, SD.

Vận dụng 1: Một chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn (H.4.20). Hỏi có thể đặt

chiếc gậy đó song song với một trong các mép tường hay không?

Lời giải:

Chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn với mép tường tạo thành hai đường thẳng

chéo nhau nên không thể song song

Hoạt động 2: Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d

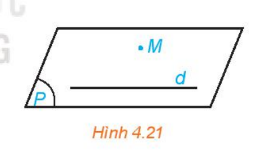
a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d?

b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?

Lời giải:

a) Có duy nhất một đường thẳng đi qua M song song với d

b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) vì hai đường thẳng song song đồng phẳng

Hoạt động 3: Quan sát lớp học và tìm hai đường thẳng song song với mép trên của bảng. Hai đường thẳng đó có

song song với nhau hay không?

Lời giải:

Đường thẳng song song với mép trên của bảng: Mép dưới của bảng, chân tường bục giảng

Hai đường thẳng đó cũng song song với nhau

Giải Toán 11 trang 81

Luyện tập 3: Trong Ví dụ 1, chứng minh rằng bốn điểm C, D, E, F đồng phẳng và tứ giác CDEF là hình bình hành.

Lời giải:

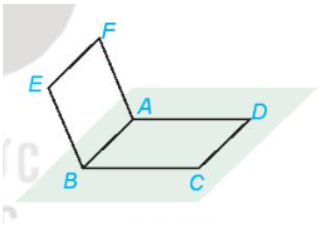
Hình bình hành ABCD ta có: AB // CD, AB = CD

Hình bình hành ABEF ta có: AB // EF, AB = EF

=> EF//CD, EF = CD

Vậy: CDEF là hình bình hành và C, D, E, F đồng phẳng

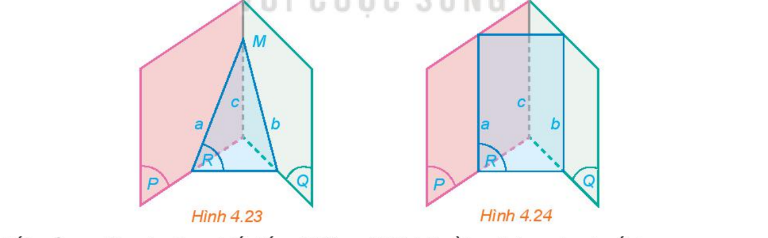
Hoạt động 4: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Một mặt phẳng (R) cắt (P) và (Q) lần lượt theo các giao tuyến a và b khác c

a) Nếu hai đường thẳng a và c cắt nhau tại M thì đường thẳng b có đi qua M hay không (H.4.23)? Giải thích vì sao.

b) Nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c có song song với nhau hay không (H.4.24)? Giải thích vì sao?

Lời giải:

a)

M thuộc c suy ra M nằm trên mp(Q)

M thuộc a suy ra M nằm trên mp(R)

M cùng thuộc mp(R) và (Q) 

=> M nằm trên giao tuyến của mp(R) và (Q)

Mà giao tuyến của mp(R) và (Q) là đường thẳng b

Vậy đường thẳng b đi qua M

b)

Ta thấy ba đường thẳng phân biệt a, b, c đôi một đồng phẳng.

Nếu không có hai trong ba đường thẳng nào trong chúng cắt nhau thì a, b, c đôi một song song.

Vậy nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c song song với nhau.

Giải Toán 11 trang 82

Luyện tập 4: Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)

Lời giải:

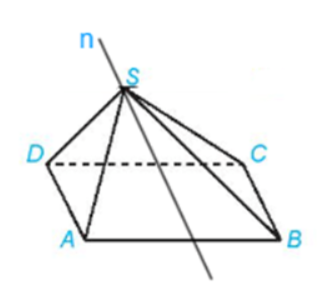
Hai mp(SAD) và (SBC) có điểm chung S 

Hai đường thẳng AD và BC song song

Vậy nên giao tuyến của hai mp(SAD) và (SBC) là đường thẳng n đi qua S song cong với AD và BC

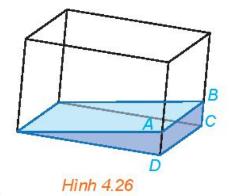
Vận dụng 2: Một bể kính chứa nước có đáy hình chữ nhật được đặt nghiêng như Hình 4.26. Giải thích tại sao

đường mép nước B song song với cạnh CD của bể nước.

Lời giải: 

mp(ABKI) ∩ mp(CDIK) = IK

mp(ABKI) ∩ mp(ABCD) = AB

mp(CDIK) ∩ (ABCD) = CD

Ta có: IK // CD (Do CDIK là hình chữ nhật) 

=>   AB // CD