Bài 19 trang 80 SGK Đại Số 10 nâng cao

Luyện tập (trang 80)

Bài 19 (trang 80 SGK Đại Số 10 nâng cao)

Giải phương trình x² + (4m + l)x + 2(m - 4) = 0, biết rằng nó có hai nghiệm và hiệu giữa nghiệm lớn và nghiệm nhỏ bằng 17.

Lời giải:

Do phương trình có hai nghiệm phân biệt nên ta có:

Δ = (4m + l)² - 8(m - 4) > 0 ⇔ 16m² + 33 > 0 đúng ∀ giá trị của m Khi đó phương trình có hai nghiệm:

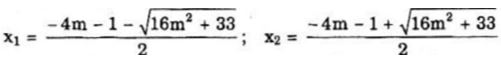
Dễ thấy x₂ > x₁, do đó:

x₂ - x₁= 17 ⇔ (2√(16m²+33))/2 = 17 ⇔ √(16m²+33) = 17

⇔ 16m² = 256 ⇔ m² = 256/ 16 = 16 → m = ± 4

Với m = 4, phương trình có hai nghiệm là:

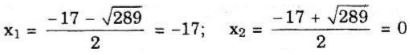
Với m = -4, phương trình có hai nghiệm là:

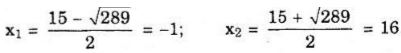
Tham khảo toàn bộ: Giải bài tập Toán 10 nâng cao