Hình bình hành là gì? Dấu hiệu nhận biết hình bình hành và các bài toán thường gặp (đầy đủ nhất)

Hình bình hành là gì? Dấu hiệu nhận biết hình bình hành và các bài toán thường gặp đầy đủ, hay nhất. Giúp các em có thể nắm vững kiến thức về hình bình hành. Hãy cùng thầy Phú toploigiai khám phá và tìm hiểu những kiến thức bổ ích qua bài viết chi tiết dưới đây!

Hình bình hành là gì?

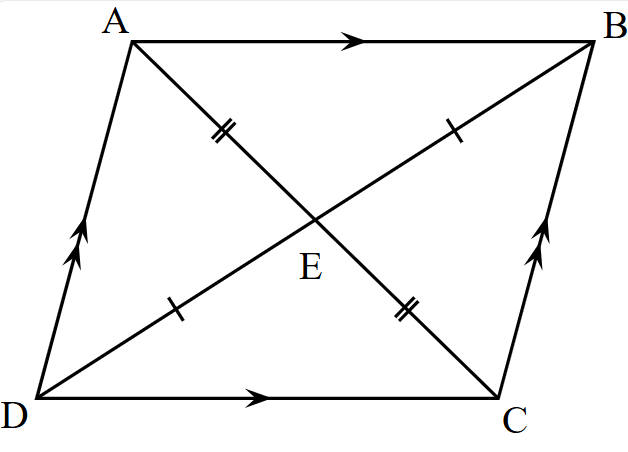
Hình bình hành trong hình học Euclid là một hình tứ giác được tạo thành khi hai cặp đường thẳng song song cắt nhau. Nó là một dạng đặc biệt của hình thang gồm 4 góc và có những tính chất giống hình thang và hình chữ nhật. Hình bình hành không phải là hình thang vì định nghĩa của hình thang yêu cầu chỉ một cặp cạnh song song.

Trong không gian 3 chiều, khối tương đương với hình bình hành là hình khối lục diện.

Ví dụ: Cho hình bình hành ABCD từ đó ta sẽ được cặp: AB//CD và AC// BD

Dấu hiệu nhận biết hình bình hành

- Hình bình hành là một tứ giác đặc biệt với các tính chất và dấu hiệu nhận biết sau:

+ Các cạnh đối song song: Nếu tứ giác có hai cặp cạnh đối diện song song với nhau, đó là hình bình hành.

+ Các cạnh đối bằng nhau: Tứ giác có hai cặp cạnh đối diện bằng nhau cũng là hình bình hành.

+ Các góc đối bằng nhau: Nếu tứ giác có các góc đối diện bằng nhau, đó là dấu hiệu của hình bình hành.

+ Đường chéo cắt nhau tại trung điểm: Hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường chéo.

+ Các cạnh đối song song và bằng nhau: Tứ giác nếu có cặp cạnh đối vừa song song và vừa bằng nhau thì đó là hình bình hành.

Chú ý: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song)

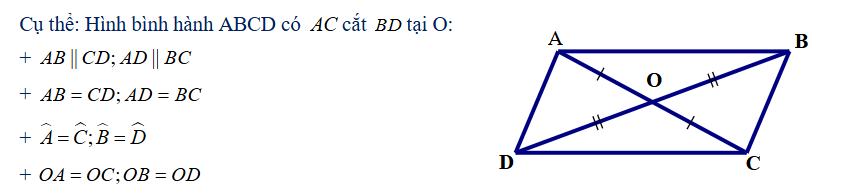
Tính chất hình bình hành

- Trong hình bình hành:

+ Các cạnh đối bằng nhau.

+ Các góc đối bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Ví dụ:

- ABCD là hình bình hành, AC cắt BD tại O. Khi đó:

+ AB = CD, AD = BC

+

+ OA = OC, OB = OD

Bài tập và các dạng toán về hình bình hành thường gặp 

Dạng 1: Vận dụng tính chất hình bình hành để chứng minh tính chất hình học và tính toán.

Phương pháp:

- Sử dụng tính chất hình bình hành:

- Trong hình bình hành:

+ Các cạnh đối bằng nhau

+ Các góc đối bằng nhau

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường 

Bài 1: Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB và CD

a. Chứng minh: AF // CE

b. Gọi M, N theo thứ tự là giao điểm của BD với AF, CE. Chứng minh: DM = MN = NB

Đáp án

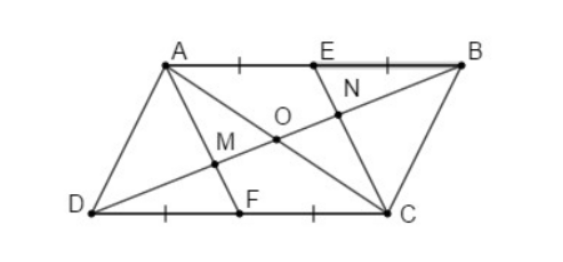
a. Vì ABCD là hình bình hành:

⇒ AB = CD (tính chất)

mà E thuộc AB và F thuộc DC ⇒ AE // FC

Vì E, F là trung điểm của AB và CD

⇒ AE = EB = DF = FC

Xét tứ giác AECF có:

AE = FC và AE // FC

⇒ AECF là hình bình hành (DHNB) ⇒ AF // EC (tính chất)

b. Gọi AC giao BD tại O

Xét tam giác ADC có:

DO, AF là trung tuyến (AO = OC, DF = FC)

AF giao DO tại M

⇒ M là trọng tâm của tam giác ADC

⇒ DM = 2/3 DO = 2/3 BO (1)

và OM = 1/3 DO = 1/3 BO (2) (do DO = BO)

Xét tam giác ABC có:

BO, CE là trung tuyến

BO giao CE tại N

⇒ N là trọng tâm của tam giác ABC

⇒ BN = 2/3 BO (3)

và ON = 1/3 BO (4)

Từ (2), (4) ⇒ MN = OM + ON = 1/3 BO + 1/3 BO = 2/3 BO (5)

Từ (1), (3) và (5) ⇒ DM = BN = MN

Bài 2: Hình bình hành ABCD, O là giao điểm của hai đường chéo, E và F theo thứ tự là trung điểm của OD và OB.

a. Chứng minh: AE // CF

b. Gọi AE giao CD tại K. Chứng minh: DK = 1/2 KC

Đáp án

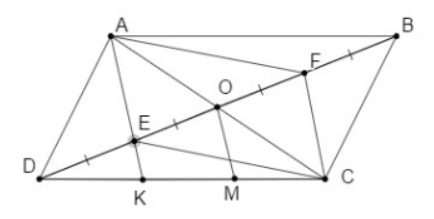
a. AC giao BD tại O ⇒ OD = BO

Vì E, F là trung điểm của DO và BO ⇒ DE = EO = OF = FB

Xét tứ giác AFCE có:

AC giao EF tại O

OA = OC

OE = OF

⇒ AFCE là hình bình hành (DHNB)

⇒ AE // CF (tính chất)

b. Từ O kẻ OM // EK

Xét tam giác DOM có:

OM // EK

và E là trung điểm của DO

⇒ K là tung điểm của DM ⇒ DK = KM (1)

Xét tam giác CDK có:

OM // AK

và O là trung điểm của AC

⇒ M là trung điểm của KC ⇒ CM = KM (2)

Từ (1) và (2) ⇒ DK = KM = CM

mà KM + CM = KC

⇒ DK = 1/2 KC

Dạng 2: Vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình bình hành.

Phương pháp: vận dụng các dấu hiệu nhận biết để chứng minh một tứ giác là hình bình hành

Bài 3. Tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của BD, AB, AC, CD.

a. Chứng minh: EFGH là hình bình hành

b. Cho AD = a, BC = b. Tính chu vi hình hình hành EFGH

Đáp án

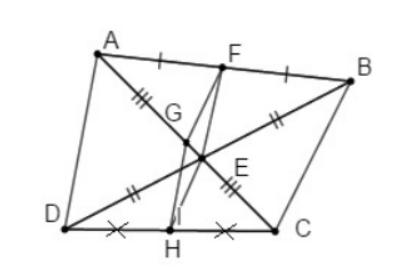
a. Xét tam giác ABD có:

F và E lần lượt là trung điểm của AB, BD ⇒ EF là đường trung bình của tam giác ABD

⇒ EF // AD (1)

và EF = 1/2 AD (2)

Tương tự, ta có GH là đường trung bình của tam giác ACD

⇒ GH // AD (3)

và GH = 1/2 AD (4)

Từ (1) và (3) ⇒ EF // GH

(2) và (4) ⇒ EF = GH

⇒ tứ giác GHEF là hình bình hành

b. Ta có: GH = EF = 1/2 AD = 1/2 a

FG = HE = 1/2 BC = 1/2 b

Chu vi hình binh hành GFEH là:

C = (1/2 a + 1/2 b) .2 = a + b

Bài 4: Cho tam giác ABH, trực tâm H. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau tại D. Chứng minh:

a. BDCH là hình bình hành

b. góc BAC + góc BDC = 180°

c. H, M, D thẳng hàng (M là trung điểm BC)

Đáp án

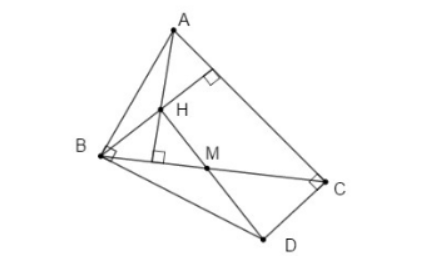
a. Ta có: CH vuông góc AB

và BD vuông góc AB

⇒ CH // DB (1)

Lại có: BH vuông góc AC

và CD vuông góc AC

⇒ BH // CD (2)

Từ (1) và (2) ⇒ BHCD là hình bình hành (DHNB)

b. Tứ giác ABCD có:

góc BAC + góc ABD + góc BDC + góc ACD = 360°

⇒ góc BAC + 90° + góc BDC + 90° = 360°

⇒ góc BAC + góc BDC = 180°

c. Vì BHCD là hình bình hành nên BC cắt HD tại trung điểm của mỗi đường

Ta có: M là tung điểm của BC

⇒ M là trung điểm của HD

⇒ H, M, D thẳng hàng

Dạng 3: Chứng minh 3 điêm thẳng hàng, các đường đồng quy

Phương pháp giải: Vận dụng các tính chất về đường chéo cả hình bình hành

Bài 5: Hình bình hành ABCD. Lấy N thuộc AB, M thuộc CD sao cho AN = CM. Chứng minh:

a. AM // CN

b. DN = BM

c. AC, BD, MN đồng quy

Đáp án

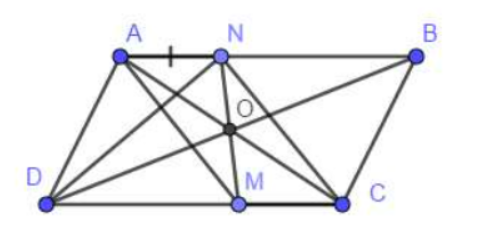
a. Xét tứ giác ABCD có:

AN = CM

AN // CM (do AB//CD)

⇒ ANCM là hình bình hành

⇒ AM // CN

b. Ta có: BN = AB - AN

DM = DC - CM

mà AB = DC, AN = CM

⇒ BN = DM

mà  BN // DM (do AB // CD)

⇒ BNDM là hình bình hành (DHNB)

⇒ DN = BM (tính chất)

c. Gọi AC giao BD tại O (1)

⇒ O là trung điểm của AC và BD

Ta có: ANCM là hình bình hành và O là trung điểm cua đường chéo Ac

⇒ O là trung điểm của MN

⇒ O thuộc MN (2)

Từ (1) và (2) ⇒ AC, BD, MN đồng quy

Bài 6: Một mảnh đất hình bình hành có cạnh đáy là 47m, mở rộng mảnh dất bằng cách tăng cạnh đáy của hình bình hanh thêm 7m, thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189 m2. Tính diện tích mảnh đất ban đầu?

Đáp án

Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy 7m và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.

Chiều cao mảnh đất là: 189 ; 7 = 27m

Diện tích mảnh đất hình bình hành ban đầu là: S = 27 . 47 = 1269 m2

Tham khảo thêm: Công thức diện tích hình bình hành khi biết hai đường chéo