Định nghĩa và cách giải về bất phương trình bậc nhất một ẩn

Tổng hợp kiến thức về định nghĩa cùng với cách giải bất phương trình một ẩn đầy đủ, hay nhất. Giúp các em có thể nắm vững kiến thức về bất phương trình một ẩn. Hãy cùng thầy Phú toploigiai khám phá và tìm hiểu những kiến thức bổ ích qua bài viết chi tiết dưới đây!

1. Bất phương trình bậc nhất một ẩn

* Định nghĩa: Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b ≥ 0, ax + b < 0) trong đó a,b là hai số đã cho, a ≠ 0 được gọi là bất phương trình bậc nhất một ẩn x.

- Với bất phương trình bậc nhất có ẩn là x, số xo được gọi là một nghiệm của bất phương trình nếu ta thay x = xo thì nhận được một khẳng định đúng. Giải phất phương trình là tìm được tất cả các nghiệm của nó.

2. Cách giải bất phương trình bậc nhất 1 ẩn

Áp dụng hai quy tắc biến đổi bất phương trình

+ Quy tắc chuyển vế

Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.

Ví dụ: Giải bất phương trình x - 3 < 4.

Lời giải:

Ta có x - 3 < 4

⇔ x < 4 + 3 (chuyển vế - 3 và đổi dấu thành 3)

⇔ x < 7.

Vậy tập nghiệm của bất phương trình là { x| x < 7 }.

+ Quy tắc nhân với một số

Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:

- Giữ nguyên chiều bất phương trình nếu số đó dương.

- Đổi chiều bất phương trình nếu số đó âm.

Ví dụ: Giải bất phương trình (x - 1)/3 ≥ 2.

Lời giải:

Ta có: (x - 1)/3 ≥ 2

⇔ (x - 1)/3.3 ≥ 2.3 (nhân cả hai vế với 3)

⇔ x - 1 ≥ 6 ⇔ x ≥ 7.

Vậy tập nghiệm của bất phương trình là { x| x ≥ 7 }.

* Bất phương trình bậc nhất một ẩn ax + b < 0 (a≠0) được giải như sau: 

ax + b < 0 => ax < −b

- Nếu a > 0 thì x<−ba

- Nếu a < 0 thì x > −ba.

Chú ý: Các bất phương trình ax+b<0, ax+b>0, ax+b≤0, ax+b≥0 được giải tương tự.

Ví dụ: Giải bất phương trình −2x−4>0

Lời giải: 

Ta có:

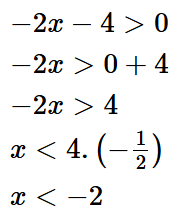
Vậy nghiệm của bất phương trình là x < −2

Chú ý: Ta cũng có thể giải được các bất phương trình một ẩn đưa được về dạng ax+b<0, ax+b>0, ax+b≤0, ax+b≥0

2. Bài tập tự luyện

Bài 1: Thực hiện các hoạt động sau

- Trong các bất phương trình sau, em hãy cho biết bất phương trình nào là bất phương trình bậc nhất một ẩn:

(1) 2x - 3 < 0 ;                                  (2) 0x + 5 > 0 ;

(3) 5x - 15 ≥ 0                                  (4) x^{2} > 0.

- Em hãy lấy thêm hai ví dụ về bất phương trình bậc nhất một ẩn.

Lời giải

- Các bất phương trình (1), (3) là bất phương trình bậc nhất một ẩn.

- Ví dụ:

t + 3 < 7

m - 5 > 8

Bài 2: Giải bất phương trình bậc nhất một ẩn sau: 0,2x - 0,2 ≥ 0,4x - 2.

Lời giải:

Ta có: 0,2x - 0,2 ≥ 0,4x - 2

      ⇔ 2 - 0,2 ≥ 0,4x - 0,2x

      ⇔ 1,8 ≥ 0,2x

      ⇔ 9 : 5 ≥ x : 5

      ⇔ 9 ≥ x 

Vậy bất phương trình có nghiệm là x ≤ 9

Bài 3: Tìm sai lầm trong các "lời giải" sau:

a) Giải bất phương trình - 2x > 23

Ta có: - 2x > 23 ⇔ x > 23 + 2 ⇔ x > 25

Vậy nghiệm của bất phương trình là x > 25.

b) Giải bất phương trình - 37x > 12

Ta có:  - 37 x > 12 ⇔ (- 73).( - 37) > (- 73).12 ⇔ x > - 28

Vậy nghiệm của bất phương trình là x > - 28.

Lời giải:

a) Lời giải trên ở chỗ - 2x > 23 ⇔ x > 23 + 2 ⇔ x > 25

Ta cần sửa lại là: - 2x > 23 ⇔ x < 23 : (- 2) ⇔ x < −232

Vậy nghiệm của bất phương trình là x < −232

b) Lời giải trên ở chỗ - 37 x > 12 ⇔ (- 73).( - 37) > (- 73).12 ⇔ x > - 28

Ta cần sửa lại là: - 37 x > 12 ⇔ (- 73).( - 37) < (- 73).12 ⇔ x < - 28

Vậy nghiệm của bất phương trình là x < - 28

Bài 4: Giải các bất phương trình sau:

8x + 3(x + 1) > 5x - (2x - 6) 

Bài làm:

Ta có: 8x + 3(x + 1) > 5x - (2x - 6) 

         ⇔ 8x + 3x + 3 > 5x - 2x + 6

         ⇔ 8x + 3x - 5x + 2x > 6 - 3

         ⇔ 8x > 3

         ⇔ x > 38

Vậy nghiệm của phương trình là x > 38.

Bài 5: Trong các bất phương trình sau, hãy cho biết bất phương trình nào là bất phương trình bậc nhất một ẩn:

a) 2x – 3 < 0;

b) 0.x + 5 > 0;

c) 5x – 15 ≥ 0;

d) x2 > 0.

Lời giải

– Bất phương trình a), c) là các bất phương trình bậc nhất một ẩn.

– Bất phương trình b) có a = 0 không thỏa mãn điều kiện a ≠ 0 nên không phải là bất phương trình bậc nhất một ẩn.

– Bất phương trình d) có mũ ở ẩn x là 2 nên không phải là bất phương trình bậc nhất một ẩn.

Bài 6: Giải các bất phương trình sau:

a) x + 12 > 21;

b) -2x > -3x – 5.

Lời giải

a) x + 12 > 21 ⇔ x > 21 – 12 ⇔ x > 9

Vậy tập nghiệm của bất phương trình x + 12 > 21 là {x|x > 9}

b) -2x > -3x – 5 ⇔ -2x + 3x > -5 ⇔ x > -5

Vậy tập nghiệm của bất phương trình -2x > -3x – 5 là {x|x > -5}

Xem thêm: >>> 5 dạng toán bất bất phương trình bậc nhất một ẩn thường gặp