5 dạng toán bất bất phương trình bậc nhất một ẩn thường gặp (hay nhất)

Hướng dẫn giải 5 dạng toán bất phương trình bậc nhất một ẩn thường gặp đầy đủ, hay nhất. Giúp các em có thể nắm vững kiến thức về bất phương trình bậc nhất một ẩn. Hãy cùng thầy Phú toploigiai khám phá và tìm hiểu những kiến thức bổ ích qua bài viết chi tiết dưới đây!

Dạng 1. Kiểm tra x = a có phải là nghiệm của bất phương trình không?

Phương pháp giải: Bằng cách thay x = a vào hai vế của bất phương trình, nếu được một bất đẳng thức đúng thì x = a là nghiệm của bất phương trình, còn nếu bất đẳng thức sai thì x = a không là nghiệm của bất phương trình.

Ví dụ: Kiểm tra xem giá trị x = 3 là nghiệm của bất phương trình nào trong các bất phương trình sau:
a) 2x + 3 < 9
b) - 4x > 2x + 5
c) 5 - x > 3x - 12

a) Thay x = 3 vào hai vế của bất phương trình ta có

 VT = 2.3 + 3 = 9 ; VP = 9 

Vậy x = 3 không là nghiệm của bất phương trình.

b) Với x = 3 ta có: 

VT = - 4.3 = - 12 VP = 2.3 + 5 =11.

Vì -12<11 nên x = 3 không là nghiệm của bất phương trình.

c) Với x = 3 ta có: VT = 5 - 3 = 2 VP = 3.3 - 12 =-3.

Vì 2 > - 3 nên x = 3 là nghiệm của bất phương trình.

Dạng 2. Biểu diễn tập nghiệm bất phương trình

Phương pháp giải

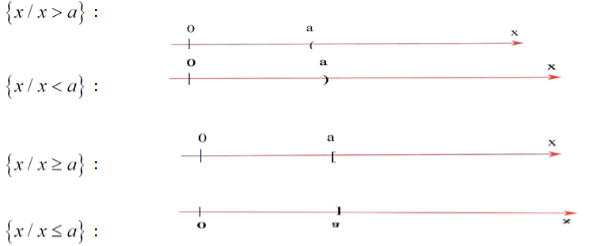
Ví dụ 1:

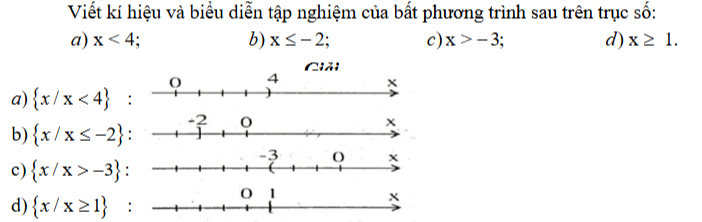
Ví dụ 2:

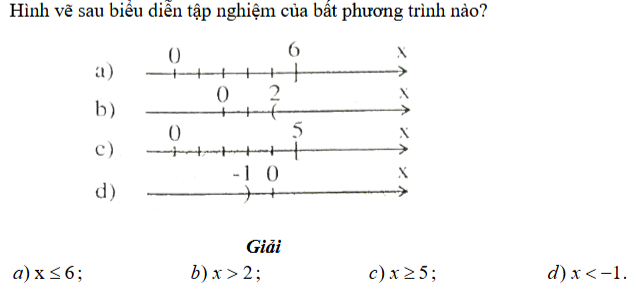
Dạng 3: Giải bất phương trình

Phương pháp giải

Bước 1: Áp dụng quy tắc nhân và quy tắc chuyển vế

Bước 2: Viết tập nghiệm của bất phương trình

Ví dụ:

Dạng 4: Bất phương trình tương đương

Phương pháp giải

• Hai bất phương trình gọi là tương đương nếu chúng có cùng tập nghiệm
• Các quy tắc chuyển về và quy tắc nhân biến đổi bất phương trình mới tương đương với bất phương trình ban đầu.

Ví dụ: Giải thích sự tương đương sau:

Dạng 5: Bài toán có lời văn 

Phương pháp giải

Bước 1: Gọi x là ẩn cần tìm, tìm điều kiện cho x.

Bước 2: Lập bất phương trình theo yêu cầu của đề bài.

Bước 3: Giải bất phương trình để tìm x.

Ví dụ 1: Một người có số tiền không quá 70000 đồng gồm 15 tờ giấy bạc với hai loại mệnh giá : loại 2000 đồng và loại 5000 đồng. Hỏi người đó có bao nhiêu tờ giấy bạc loại 5000 đồng.
Lời giải

Gọi x là số tờ giấy bạc loại 5000 đồng (x nguyên dương).
Số tờ giấy bạc loại 2000 đồng là : 15-x
Số tiền người đó có : 5000x + 2000(15-x).
Theo đề bài ta có :

Xem thêm: >>> Định nghĩa và cách giải về bất phương trình bậc nhất một ẩn