Giải Toán 10 Kết nối tri thức: Bài 6: Hệ thức lượng trong tam giác

Hướng dẫn Giải Toán 8 Kết nối tri thức Bài 6: Hệ thức lượng trong tam giác ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 10 trang 38

Hoạt động 1: Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20km/h. Sau

khi đi được 1 giờ, tàu chuyển sang hướng Đông Nam rồi giữ nguyên vận tốc và đi tiếp.

a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1cm trên bản vẽ).

b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu

kilômét (số đo gần đúng).

c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng Định lí

Pythagore (Pi – ta – go) để tính chính xác các số đo trong câu b hay không?

Lời giải

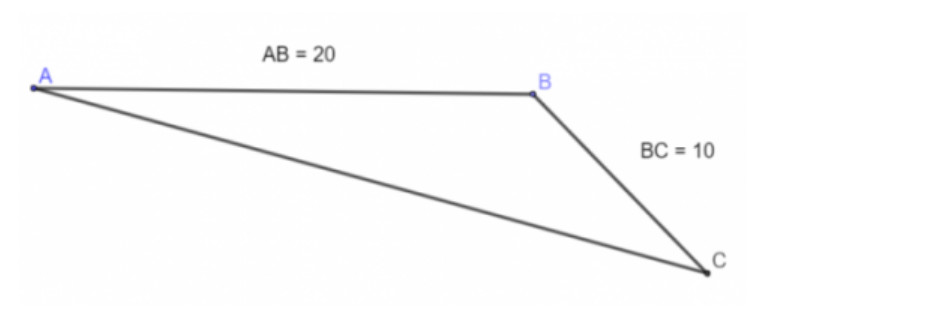
a. Hình vẽ thể hiển sơ đồ đường đi của tàu, tàu xuất phát từ cảng Vân Phong (điểm A), đi theo hướng từ A đến B,

sau đó từ B chuyển hướng đi C (hướng đông nam). Thời gian đi từ B đến C là 0,5 giờ.

b. Khoảng cách từ C đến A khoảng 28 cm, thì thực tế tàu cách cảng Vân Phong 28 km

c. Có thể dùng Định lí Pythagore (Pi-ta-go) vì nếu tàu chuyển hướng sang nam thì góc ABC là góc vuông, ta có thể

áp dụng định lí Pythagore (Pi-ta-go).

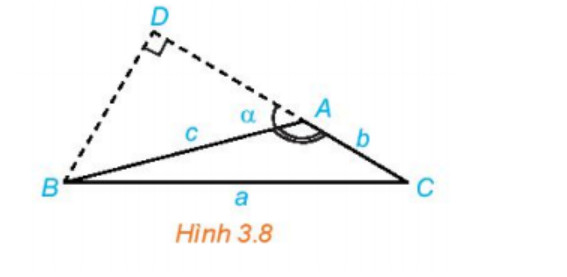
Hoạt động 2: Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b, c và giá trị lượng

giác của góc A.

a. Tính a² theo BD² và CD² .

b. Tính a² theo b, c và DA.

c. Tính DA theo c và cos A.

d. Chứng minh a² = b² + c² - 2b.c.cos A.

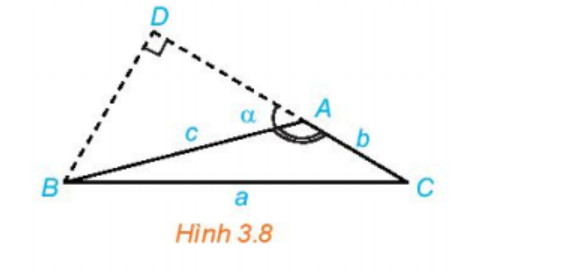
Lời giải

a. a² = BD² + CD² (áp dụng định lí Pitago cho tam giác vuông BDC).

b. a² = c² – DA² + (DA + b)² = c² – DA² + (DA² +2.b.DA + b² )= c² +2.b.DA + b²

c. DA = c. cosα = c.(-cos A) = -c.cos A

d. Theo b ta có: a² =  c² + 2.b.DA + b²  (1) , thay DA = -c.cos A vào (1) ta được:

a² = b² + c² -2b.c.cos A.

Giải Toán 10 trang 39

Luyện tập 1: Cho tam giác ABC, có AB = 5, AC = 8 và ˆA=45°. Tính độ dài các cạnh và độ lớn các góc còn lại của

tam giác.

Lời giải

Áp dụng định lí cosin cho tam giác ABC có: 

BC² = AB² + AC² – 2AB.AC.cos45^o = 5² + 8² − 2.5.8.1/√2 ≈ 32

⇒ BC ≈ 5,7

Ta có: AC² = AB² + BC² – 2AB.BC.cos B

⇒ cosB ≈ −0,123

⇒ B ≈ 97^o

⇒ C ≈ 38^o

Hoạt động 3: Trong mỗi hình dưới đây, hãy tính R theo a và sin A.

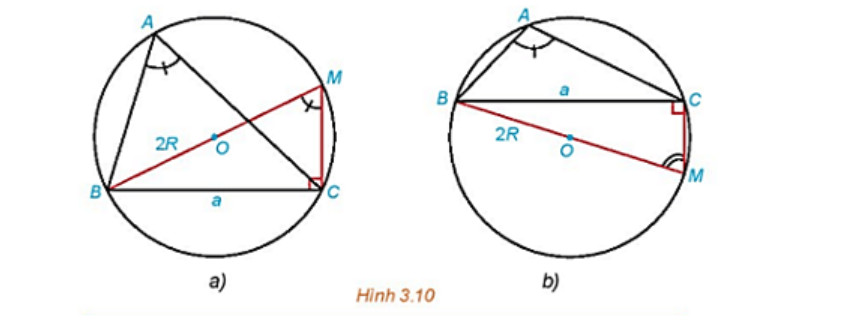
Lời giải

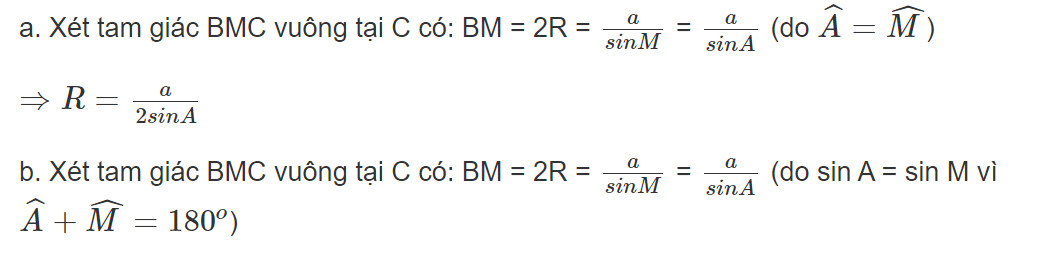
Giải Toán 10 trang 40

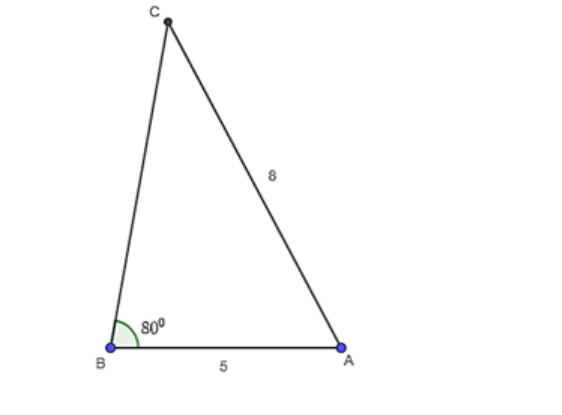
Luyện tập 2: Cho tam giác ABC có b = 8, c = 5 và Aˆ=80o. Tính số đo các góc, bán kính đường tròn ngoại tiếp và

độ dài cách cạnh còn lại của tam giác

Lời giải

Luyện tập 3: Giải tam giác ABC, biết b = 32, c = 45,  ˆA = 87⁰

Lời giải

Xét ΔABC, có:

Theo định lý Cos, ta có:

BC² = AB² + AC² – 2.AB.AC.cosA

= 32² + 45² – 2.32.45.cos87⁰ ≈ 2898,27

=> BC ≈ 53,84

Theo định lí Sin, ta có:

a/sinA = b/sinB = c/sinC = 2R 

⇒ 53,84/sin87⁰ = 32/sinB = 45/sinC ⇒ 

53,84/sin87⁰ = 32/sinB ⇒ sinB = 0,59

⇔ góc B=36,40

⇒ góc C=56,60

Vậy góc B=36,40, góc C = 56,60 và BC = 53,84.

Giải Toán 10 trang 41

Hoạt động 4: Cho ΔABC với I là tâm đường tròn nội tiếp tam giác.

a) Nêu mối liên hệ giữa diện tích tam giác ABC và diện tích tam giác IBC, ICA, IAB.

b) Tính diện tích tam giác ABC theo r, a, b, c.

Lời giải

a) Ta có diện tích tam giác ABC bằng tổng diện tích tam giác IAB, IAC, IBC: S∆ABC = S_∆IBC + S_∆ICA + S_∆IAB

b) Ta có:

S_ΔIBC = 1/2a.r

S_ΔICA=1/2b.r

S_ΔIAB = 1/2c.r

⇒ S_ΔABC = S_ΔIBC + S_ΔICA + S_ΔIAB = 1/2a.r + 1/2b.r + 1/2c.r = [(a+b+c).r]/2.

Vậy SΔABC=[(a+b+c).r]/2.

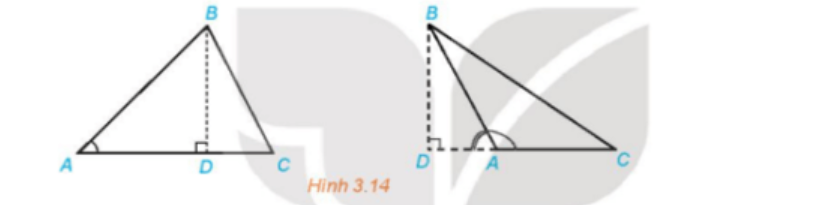
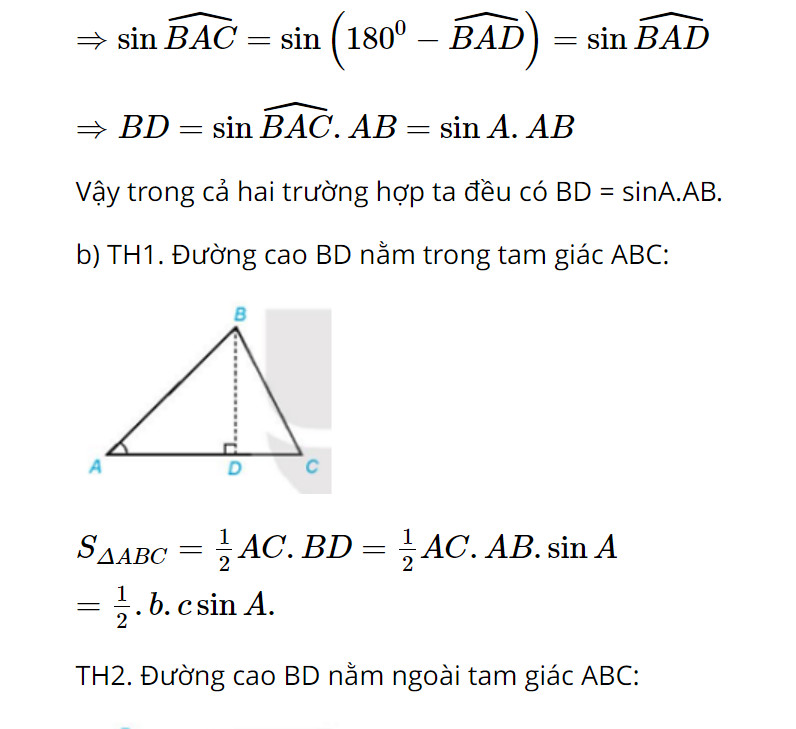
Hoạt động 5: Cho tam giác ABC với đường cao BD

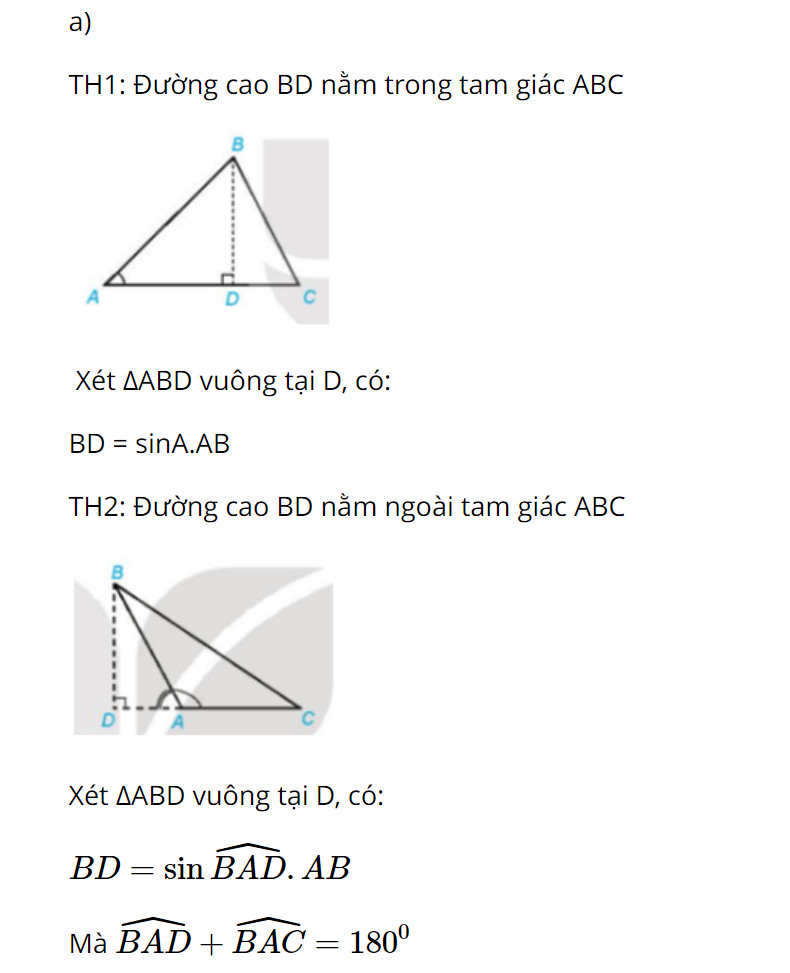
a) Biểu thị BD theo AB và sin A.

b) Viết công thức tính diện tích S của tam giác ABC theo b, c, sin A

Lời giải

Luyện tập 4: Tính diện tích tam giác ABC có b = 2, ˆB = 30⁰,ˆC = 45⁰.

Lời giải

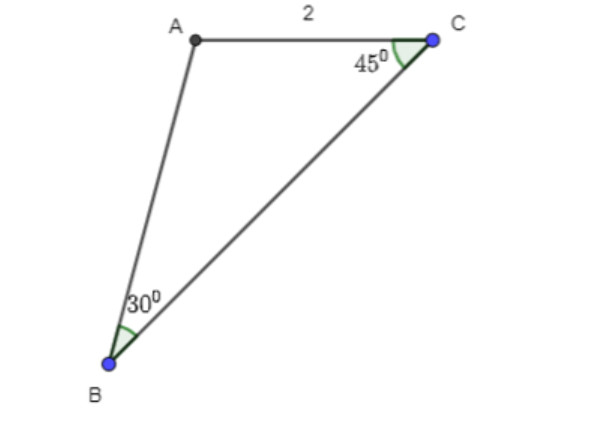
Xét ΔABC ta có:

Theo định lí sin, ta có: 

AC/sinB = AB/sinC ⇔ 2/sin 30⁰ = AB/sin45⁰ ⇔ AB =( 2.sin45⁰)/sin30⁰ = 2√2.

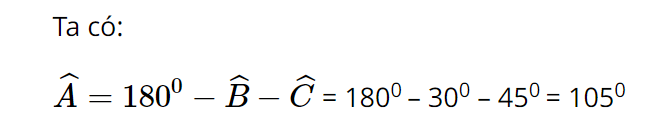
Diện tích tam giác ABC là:

S_ΔABC = 1/2.AB.AC.sinA

 = 1/2.2√2.2.sin105⁰

=1+√3(đvdt)

Vậy diện tích tam giác ABC là 1+√3(dvdt)