Bài 7: Các khái niệm mở đầu

Hướng dẫn Giải Toán 8 Kết nối tri thức Bài 7: Các khái niệm mở đầu ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 10 trang 47

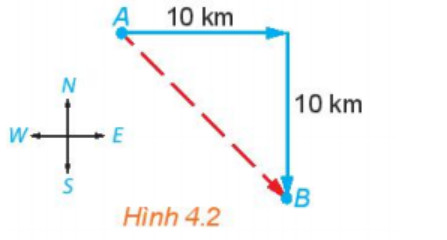
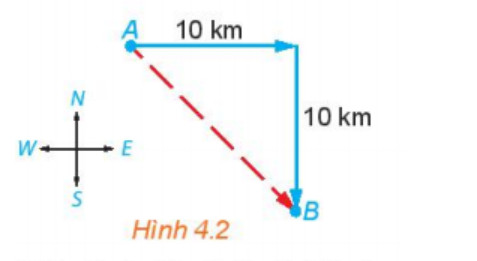
Hoạt động 1: Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km về hướng nam thì tới đảo B. Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải theo hướng nào và quãng đường phải đi dài bao nhiêu kilomet?

Lời giải

Vì góc giữa hướng đông và hướng nam là bằng 900 nên ˆAHB = 90⁰

Xét ∆AHB vuông ở H, ta có:

AB² = AH² + BH² (định lí Py – ta – go)

AB² = 10² + 10² = 100 + 100 = 200

⇔ AB = 10√2(km)

∆AHB vuông tại H, có AH = BH = 10 km nên ∆AHB cân tại H

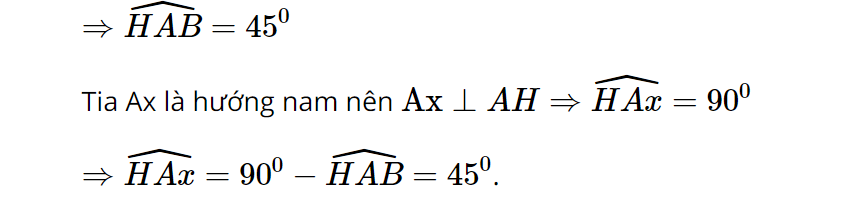
Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng đông nam và đi quãng đường dài 10√2km.

Luyện tập 1: Cho tam giác đều ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vectơ có độ dài bằng a và có điểm

đầu, điểm cuối là các đỉnh của tam giác ABC.

Lời giải

Vì tam giác ABC là tam giác đều nên ta có:

AB = AC = BC = a.

Do đó các vectơ có độ dài bằng a và có điểm đầu và điểm cuối là các đỉnh của tam giác ABC là:

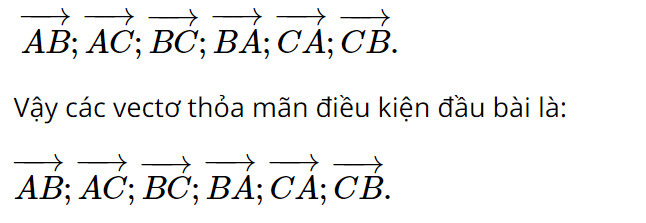
Hoạt động 2: Quan sát các làn đường trong Hình 4.5 và cho biết những nhận xét nào sau đây là đúng:

a. Các làn đường song song với nhau.

b. Các xe chạy theo cùng một hướng.

c. Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau.

Lời giải

Sau khi quan sát hình vẽ, ta có nhận xét sau:

- Phát biểu a) đúng. Vì các làn đường chạy song song với nhau.

 - Phát biểu b) sai. Vì có ba xe hướng từ trên xuống dưới, còn hai xe hướng từ dưới lên trên.

-  Phát biểu c) đúng. Vì hai xe bất kì hoặc chạy cùng hướng hoặc chạy ngược hướng nhau.

Giải Toán 10 trang 48

Hoạt động 3: Xét các vecto cùng phương trong Hình 4.7. Hai vecto a và AB được gọi là cùng hướng, còn hai

vecto a và x được gọi là ngược hướng. Hãy chỉ ra các vecto cùng hướng với vecto a và các vecto ngược hướng

với vecto a.

Lời giải

- Theo quan sát hai vecto a và AB ta thấy hai vecto cùng hướng thỏa mãn điều kiện cùng phương (giá song song)

và cùng hướng lên trên.

Vì vậy các vecto cùng hướng với vecto a,AB và y

- Theo quan sát hai vecto a và x ta thấy hai vecto ngược hướng thỏa mãn điều kiện cùng phương (giá song song)

và vecto a hướng lên trên còn vecto x lại hướng xuống dưới. 

Vì vậy các vecto ngược hướng với vecto a là x và z.

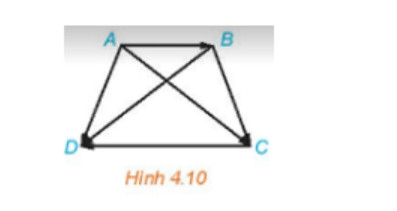
Luyện tập 2: Cho hình thang cân ABCD với hai đáy AB, CD, AB <CD (H4.10). Hãy chỉ ra mối quan hệ về độ dài,

phương, hướng giữa các cặp vecto AD và BC, AB và CD, AC và BD. Có cặp vecto nào trong các cặp vecto trên

bằng nhau không?

Lời giải

- Vecto AD và vecto BC: độ dài bằng nhau, không cùng phương, không cùng hướng.

- Vecto AB và vecto CD: cùng phương, ngược hướng.

- Vecto AC và vecto BD: độ dài bằng nhau, không cùng phương, không cùng hướng.

- Không cặp nào là cặp vecto bằng nhau.

Luyện tập 3: Trong các điều kiện dưới đây, chọn điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B

Lời giải

Nếu điểm M nằm giữa hai điểm A và B thì MA và MB ngược hướng.

Nếu hai vecto MA và MB ngược hướng

Thì hai vecto MA và MB cùng phương

⇒MA // MB (vô lí)  hoặc MA trùng MB.

⇒ A, M, B thẳng hàng

Mà hai vecto MA và MB ngược hướng nên điểm M nằm giữa điểm A và điểm B.

Điềm M nằm giữa hai điểm A và B khi và chỉ khi MA và MB ngược hướng.

Vậy điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B là MA và MB ngược hướng.

Chọn d)