Bài 3.38 trang 73 SGK Toán 8 Tập 1 Kết nối tri thức

Luyện tập chung trang 73

Bài 3.38 trang 73 SGK Toán 8 Tập 1 Kết nối tri thức: Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M. Đường thẳng qua M vuông góc với AE cắt BC tại N. Chứng minh DM + BN = MN

Lời giải:

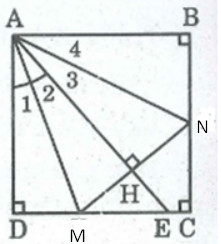
Gọi giao điểm của AE và MN là H

Xét tam giác vuông AMD và AMH ta có:

AM chung

góc A₁ = góc A₂

Suy ra ΔAMD = ΔAMH ⇒ DM = MH, AD = AH

Xét tam giác vuông ANH và ANB ta có:

AN chung

AH = AB ( do cùng = AD)

Suy ra ΔANH = ANB ⇒NH = BN

Ta có DM = MH, NH = BN ⇒ DM + BN = MH + NH = MN

* Kiến thức vận dụng giải bài tập:

Chứng minh: MD = MP; ∆ADM = ∆APM (cạnh huyền – góc nhọn).

Suy ra MD = MP (hai cạnh tương ứng).

Ta có MP + PN = MN mà MD = MP

Do đó DM + BN = MN.