Bài 3.34 trang 73 SGK Toán 8 Tập 1 Kết nối tri thức

Luyện tập chung trang 73

Bài 3.34 trang 73 SGK Toán 8 Tập 1 Kết nối tri thức: Cho tam giác ABC; M và N lần lượt là trung điểm của hai cạnh AB và AC. Lấy điểm P sao cho N là trung điểm của đoạn MP

a) Hỏi tứ giác AMCP là hình gì? Vì sao?

b) Với điều kiện nào của tam giác ABC thì tứ giác AMCP là hình chữ nhật; hình thoi; hình vuông ?

Lời giải:

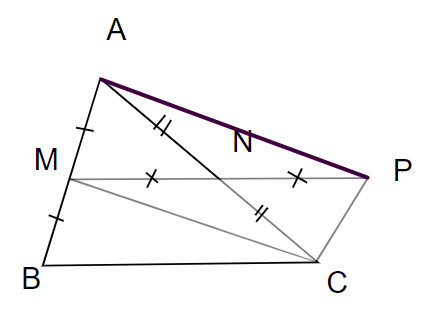
a) Xét tứ giác AMCP ta có: 

NA = NC

NM = NP 

=> AMCP là hình bình hành

b) Để AMCP là hình chữ nhật thì góc AMC = 90^∘ 

=> tam giác ABC cân tại C

Để AMCP là hình thoi thì AC⊥MP mà MN // BC ⇒ AC⊥BC 

=> tam giác ABC vuông tại C

Để AMCP là hình vuông thì AMCP là hình thoi có 1 góc bằng 90^∘ 

suy ra tam giác ABC vuông cân tại C

* Kiến thức vận dụng giải bài tập:

a) Sử dụng các dấu hiệu để chứng minh AMCP là hình bình hành

b) Sử dụng các dấu hiệu nhận biết của hình chữ nhật, hình thoi, hình vuông suy ra:

Tam giác ABC cân tại C thì hình bình hành AMCP là hình chữ nhật  

 tam giác ABC vuông tại C thì hình bình hành AMCP là hình thoi 

 tam giác ABC vuông cân tại C thì hình bình hành AMCP là hình vuông