Lý thuyết về tập hợp các số tự nhiên toán lớp 6
Tóm tắt Lý thuyết về tập hợp toán lớp 6 theo chương trình Sách mới ngắn gọn nhất. Tổng hợp lý thuyết về tập hợp Toán lớp 6 cùng các dạng bài tập và ví dụ minh họa chi tiết, đầy đủ.
Sơ đồ tư duy về tập hợp toán lớp 6
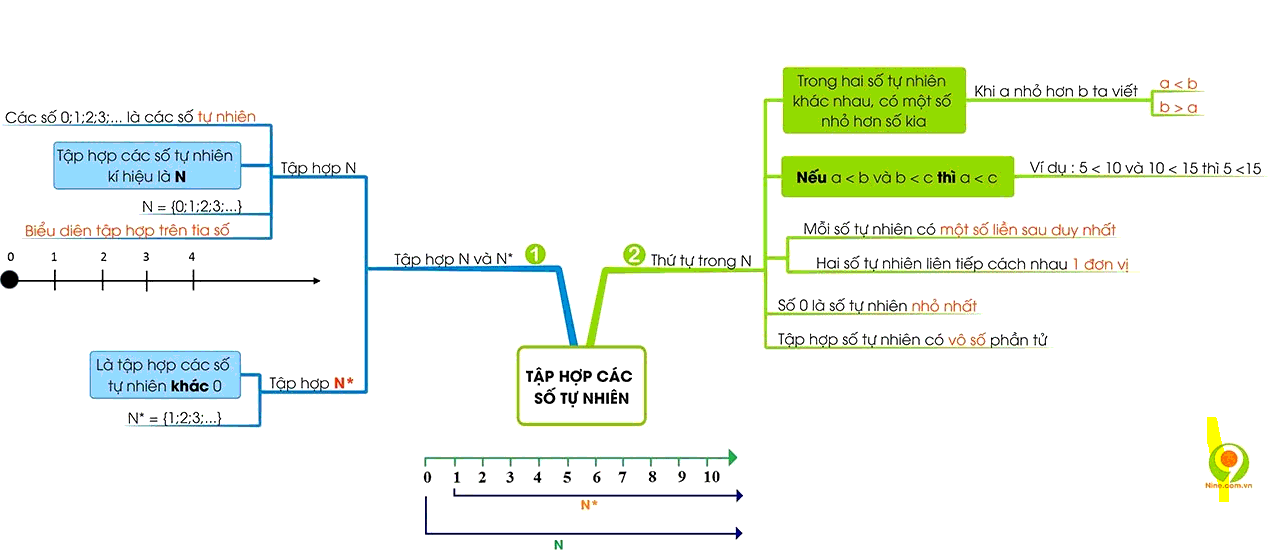
Lý thuyết về tập hợp các số tự nhiên
1. Định nghĩa
+ Tập hợp các số 0; 1; 2; 3; ... được gọi là tập hợp các số tự nhiên. Tập hợp các số tự nhiên được kí hiệu là N .
+ Tập hợp các số tự nhiên khác 0 được kí hiệu là N*.
2. Thứ tự trong tập hợp số tự nhiên
+ Các số tự nhiên được biểu dễn trên tia số. Mỗi số được biểu diễn bởi một điểm.
+ Hai số tự nhiên liên tiếp làhai số tự nhiên hơn kém nhau một đơn vị.
+ Trong hai số tự nhiên khác nhau luôn có một số nhỏ hơn số còn lại. Khi số a nhỏ hơn số b ta viết a< b hoặc b > a . Ta viết a ≤ b để chỉ a < b hoặc a = b và ngược lại a ≥ b để chỉ a >b hoặc a = b .
+ Ba số a, b, c là các số tự nhiên. Nếu a < b và b <c thì a <c .
+ Mỗi số tự nhiên có duy nhất một số liền sau.
+ Mỗi số tự nhiên có duy nhất một số liền trước (trừ số 0 )
+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị.
+ Tập hợp số tự nhiên có vô số phần tử.
+ Số 0 là số tự nhiên nhỏ nhất. Không có số tự nhiên lớn nhất.
3. Số La Mã
Các số tự nhiên từ 1 đến 10 ghi bằng số La Mã tương tứng như sau
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Nếu thêm vào bên trái mỗi số ở dòng (1) một chữ số X , ta được số La Mã từ 11 đến 20 :
XI |
XII |
XIII |
XIV |
XV |
XVI |
XVII |
XVIII |
XIX |
XX |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Nếu thêm vào bên trái mỗi số ở dòng (1) hai chữ số X , ta được số La Mã từ 21 đến 30 :
XXI |
XXII |
XXIII |
XXIV |
XXV |
XXVI |
XXVII |
XXVIII |
XXIX |
XXX |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
Cách giải bài toán về Tập hợp các số tự nhiên
Dạng 1. Tìm số tự nhiên liền trước, liền sau và số La Mã
Phương pháp giải:
+ Hai số tự nhiên liên tiếp hơn kém nhau1 đơn vị.
+ Nhớ được bảng số La Mã.
Dạng 2. Sử dụng kí hiệu ∈ và ∉
Phương pháp giải
+ Nếu a thuộc tập hợp A , ta viết a ∈ A
+ Nếu a không thuộc tập hợp A , ta viết a ∉ A
Dạng 3. Viết tập hợp các số tự nhiên thỏa mãn điều kiện cho trước
Phương pháp giải
+ Liệt kê các phần tử của tập hợp
Lưu ý: Mỗi phần tử chỉ được viết một lần vàđược ngăn cách bởi dấu “;”
+ Chỉ ra tính chất đặc trưng của các phần tử của tập hợp
Dạng 4. Xác định số phần tử và tính tổng các phần tử của tập hợp
Phương pháp giải: Thực hiện theo 2 bước:
+ Tính số phần tử: (Số cuối – số đầu) : khoảng cách + 1
+ Tính tổng: (Số cuối + số đầu) x số phần tử : 2
Trắc nghiệm về Tập hợp các số tự nhiên toán lớp 6
Câu 1. Cho hai số tự nhiên là 99;100. Hãy tìm số tự nhiên để ba số đó lập thành ba số tự nhiên liên tiếp
A. 98
B. 97
C. 101
D. Cả A và C
Đáp án D
Câu 2. Tập hợp A là tập hợp các số tự nhiên bao gồm các phần tử lớn hơn 5 và không vượt quá 8
A. A = {6; 7}
B. A = {6;7; 8}
C. A = {5; 6; 7; 8}
D. A = {7; 8}
Đáp án B
Câu 3. Viết tập hợp C = {1;2; 3; 4} dướidạng chỉ ra tính chất đặc trưng của tập hợp đó:
A. C = {x ∈ N | 0 ≤ x < 5}
B. C = {x ∈ N | 0 ≤ x ≤ 5}
C. C = {x ∈ N | 0 < x < 5}
D. C = {x ∈ N | 0 < x ≤ 5}
Đáp án C
Câu 4. Cho tập hợp
A = {x ∈ N | x < 10} và B là tập hợp các số tự nhiên không nhỏ hơn 4 và không lớn hơn 12. Chọn phương án Sai?
A. 4 ∈ B
B. Tập hợp A gồm 10 phần tử
C. Tập hợp B gồm 7 phần tử
D. Tập hợp {4; 5; 6; 7; 8;9} có tất cả các phần tử đều thuộc cả A và B
Đáp án A
Câu 5. Cho A = {2; 5; 6}. Tập hợp các số tự nhiên có hai chữ số khác nhau lấy từ tập hợp A là:
A. {25; 26; 52; 56; 62; 65}
B. {25; 26; 52; 56}
C. {25; 26; 56}
D. {25; 56}
Đáp án A
Ta có: Các số tự nhiên có hai chữ số khác nhau được lấy từ các phần tử thuộc A là: 25; 26; 52; 56; 62;65
Vậy câu A đúng.
Bài tập tự luận về Tập hợp các số tự nhiên có lời giải
Bài 1.
a. Số liền trước số 49 là số?
b. Tìm số tự nhiên a, b, c thỏa mãn 228 ≤ a < b <c ≤ 230?
Lời giải
a. Số liền trước số 49 là số 48
b. Theo đề ta có các số tự nhiên lớn hơn hoặc bằng 228 và nhỏ hơn hoặc bằng 230 là 228; 229; 230
Mặt khác a < b < c nên a = 228, b = 229, c = 230
Bài 2. Cho hai tập hợp C = {1; 2; 3} và D = {1; 3} . Hãy điền kí hiệu ∈ và ∉ thích hợp vào chỗ chấm
a) 1... C
b) 1... D
c) 2 ...C
d) 2 ... D
Lời giải
a)1 ∈C
b) 1 ∈ D
c) 2 ∈ C
d) 2 ∉ D
Bài 3. Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho phần tử của tập hợp đó.
a) A = {1; 3; 5; 7; 9}
b) B = {3; 6; 9; 12; 15; 18}
c) C = {2; 6; 10; 14; 18; 22}
Lời giải
a) A = {x | x là số tự nhiên lẻ, x < 10}
b) B = {x ∈ N* | x chia hết cho 3, x < 20}
c) C = {x | x = 4n + 2, n ∈ N, n ∈ 5}
Bài 4. Tìm số phần tử của các tập hợp sau đây:
a) A = {2; 3; 4; 5; 6; 7; 8; 9}
b) B = {2; 4; 6; 8; ...; 20}
c) C = {1; 4; 7; 10; ...; 25}
d) D = {2; 4; 6; 8; ...; 102; 104}
e) E = {5; 10; 15; 20; ...; 470}
f) F = {10; 20; 30; 40; ...; 500}
Lời giải:
a) A = {2; 3; 4; 5; 6; 7; 8; 9} có 8 phần tử
b) B = {2; 4; 6; 8; ...; 20} có 10 phần tử
c) C = {1; 4; 7; 10; ...; 25}
Khoảng cách: 3
Số phần tử: (25 -1) : 3 +1 = 9
d) D = {2; 4; 6; 8; ...; 102; 104}
Khoảng cách: 2
Số phần tử: (104 - 2) : 2 +1 = 52
e) E = {5; 10; 15; 20; ...; 470}
Khoảng cách: 5
Số phần tử: (470 - 5) : 5 +1 = 94
f) F = {10; 20; 30; 40; ...; 500}
Khoảng cách: 10
Số phần tử: (500 -10) :10 +1 = 50
