Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
Hệ thống kiến thức về hiệu hai bình phương, cách giải bài tập hiệu hai bình phương, bình phương của một tổng hay một hiệu Toán 8 chi tiết, dễ hiểu bám sát chương trình Sách mới.
1. Hằng đẳng thức là gì?
- Hằng đẳng thức là đẳng thức mà hai về luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.
- 7 hằng đẳng thức đáng nhớ là công cụ không thể thiếu trong vốn kiến thức của học sinh, nhờ việc học các hằng đẳng thức giúp các bạn học sinh rèn được các kỹ năng quan sát, nhận xét cũng như sự tỉ mỉ trong khi phân tích các vấn đề trong toán học cũng như rèn luyện các kỹ năng cẩn thận cả trong những tình huống đời thường.
7 hằng đẳng thức đáng nhớ:
1. ( a + b )2 = a2 + 2ab + b2
2. ( a - b )2 = a2 - 2ab + b2
3. a2 - b2 = ( a - b )( a + b )
4. ( a + b )3 = a3 + 3a2b + 3ab2 + b3
5. ( a - b )3 = a3 - 3a2b + 3ab2 - b3
6. a3 + b3 = ( a + b )( a2 - ab + b2 )
7. a3 - b3 = ( a - b )( a2 + ab + b2 )
2. Bình phương là gì?
Bình phương là kết quả của việc nhân một số hoặc biểu thức khác với chính nó.
3. Hiệu hai bình phương là gì?
Hiệu hai bình phương là một trong bảy hằng đẳng thức đáng nhớ. Hiệu hai bình phương bằng hiệu hai số đó nhân tổng hai số đó.
A2 – B2 = (A + B)(A – B)
4. Cách tính hiệu của hai bình phương
Bình phương của hiệu hai biểu bằng bình phương của biểu thức thứ nhất trừ hai lần tích hai biểu đó cộng bình phương của biểu thức thứ hai.
Ví dụ:
(2x+1)(2x-1) = (2x)2 -12 = 4x2 -1
912 - 92 = (91 - 9)(91 + 9) = 82.100 = 8200
(70 - 8)(70 + 8) =702 - 82 = 4900 - 64 = 4836
5. Công thức bình phương của một tổng
Bình phương của một tổng bằng bình phương số thứ nhất cộng với hai lần tích số thứ nhất nhân với số thứ hai rồi cộng với bình phương của số thứ hai.
(A + B)2 = A2 + 2AB + B2
Ví dụ:
9x2 + 12x + 4 = (3x)2 + 2.3x.2 + 22 = (3x + 2)2
9x² + y² + 6xy = (3x)² + y² + 2. 3x. y = (3x + y)²
25a² + 4b² – 20ab = (5a)² + (2b)² – 2. 5a. 2b = (5a – 2b)²
x² – x + 1/4 = x² – 2.x.1/2 +(1/2)² = (x – 1/2)²
6. Công thức bình phương của một hiệu
Bình phương của một hiệu bằng bình phương số thứ nhất trừ đi hai lần tích số thứ nhất nhân số thứ 2 rồi cộng với bình phương số thứ hai.
(A - B)2 = A2 - 2AB - B2
Ví dụ:
(2x - 1)² = (2x)² - 2.2x.1 + 1² = 4x² - 4x + 1
(3x- 2y)2 = (3x)2 - 2.3x.2y + (2y)2 = 9x2 - 12xy + 4y2
(x - xy)2 = x2 - 2.x.xy + (xy)2 = x2 - 2x22y + x2y2
(1 - 3a)2 = 12 - 2.1.3a + (3a)2 = 1 - 6a + 9a2
7. Bài tập vận dụng
Câu 1: Hãy tìm cách giúp bạn An khôi phục lại những hằng đẳng thức bị mực làm nhòe đi một số chỗ:
a) x2 + 6xy + ... = ( ... + 3y)2
b) ... - 10xy + 25y2 = ( ... - ...)2
Hãy nêu một đề bài tương tự.
Lời giải:
a) Dễ dàng nhận thấy đây là hằng đẳng thức (1).
Xét vế trái: x2 + 6xy + ... = x2 + 2.x.3y + …
Với A = x ; 2.AB = 6xy ⇒ B = 3y.
Vậy ta có hằng đẳng thức:
x2 + 2.x.3y + (3y)2 = (x + 3y)2
hay x2 + 6xy + 9y2 = (x + 3y)2
b) Nhận thấy đây là hằng đẳng thức (2) với :
B2 = 25y2 = (5y)2 ⇒ B = 5y
2.AB = 10xy = 2.x.5y ⇒ A = x.
Vậy ta có hằng đẳng thức : x2 – 10xy + 25y2 = (x – 5y)2
Câu 2: Chứng minh rằng: (10a + 5)2 = 100a . a(a + 1) + 25
Từ đó em hãy nêu cách tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số 5.
Áp dụng để tính: 252; 352; 652; 752
Lời giải :
Ta có:
(10a + 5)2 = (10a)2 + 2.10a.5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25
Đặt A = a.(a + 1). Khi đó ta có:
Do vậy, để tính bình phương của một số tự nhiên có dạng Giải bài tập Vật lý lớp 10 , ta chỉ cần tính tích a.(a + 1) rồi viết 25 vào đằng sau kết quả vừa tìm được.
Áp dụng:
252 = 625 (Vì 2.3 = 6)
352 = 1225 (Vì 3.4 = 12)
652 = 4225 (Vì 6.7 = 42)
752 = 5625 (Vì 7.8 = 56)
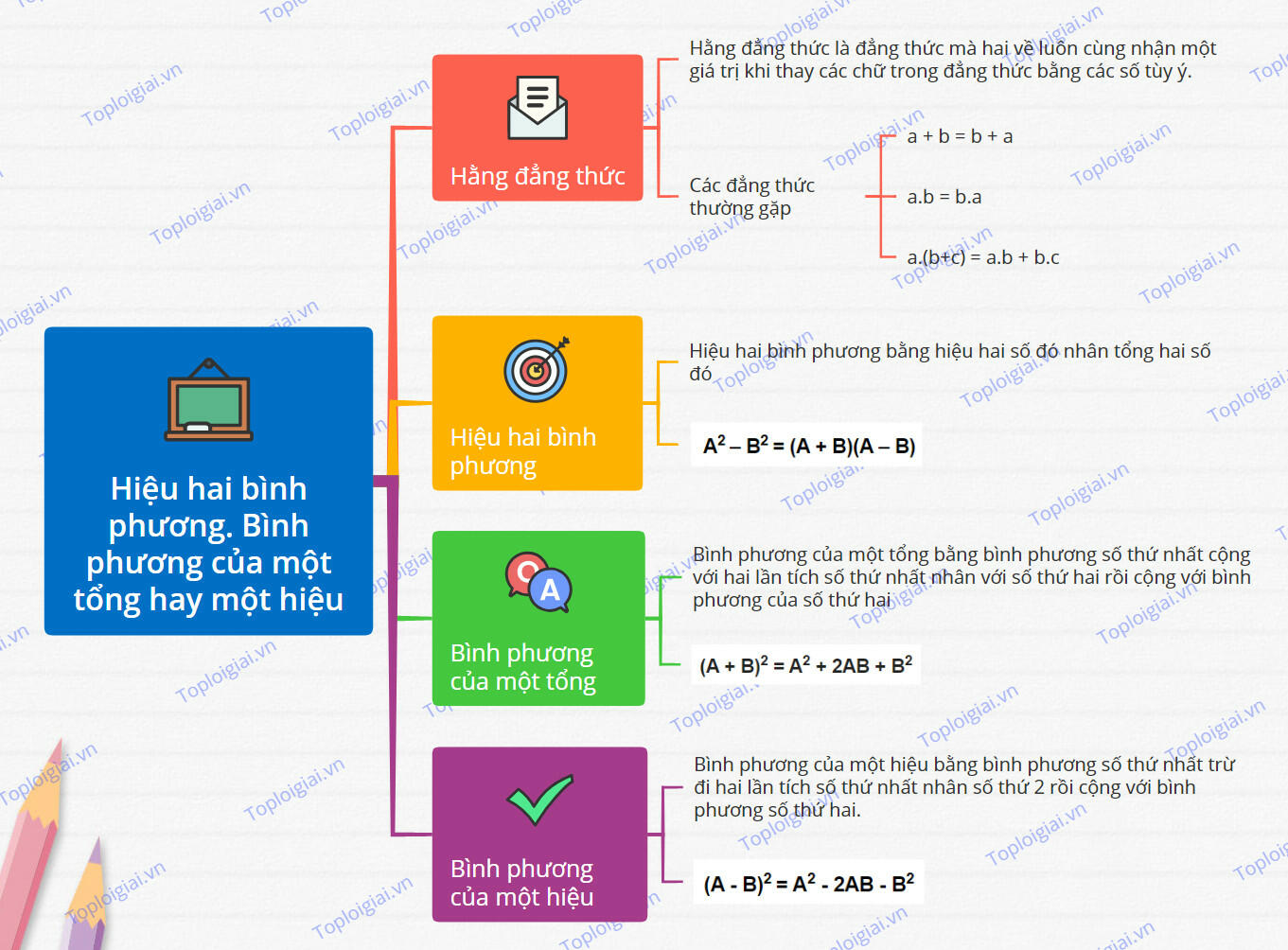
8. Sơ đồ tư duy Hiệu hai bình phương. Bình phương của một tổng hay một hiệu