Khái niệm về đa thức, cách giải bài tập đa thức

Hệ thống kiến thức về đa thức, cách giải bài tập đa thức Toán 8 chi tiết, dễ hiểu bám sát chương trình Sách mới.

Đa thức là gì?

Đa thức là tổng của những đơn thức; mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.

* Chú ý: Mỗi đơn thức cũng được gọi là một đa thức (chỉ chứa một hạng tử).

Đa thức thu gọn là gì?

Đa thức thu gọn là đa thức không có hai hạng tử nào đồng dạng.

* Chú ý: Ta thường viết một đa thức dưới dạng thu gọn (nếu không có yêu cầu gì khác).

Ví dụ về đa thức

Ví dụ đa thức: 

A = x⁴ + 2xy + 6, đa thức A có 3 hạng tử.

B = x² + 5xy + 6xy³z + 1, đa thức B có 4 hạng tử.

- Đối với các đa thức chứa hạng tử đồng dạng ta tiến hành thu gọn chúng bằng cách nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.

Ví dụ: 

A = x² + 2xy³ - 4y² + 5xy³  = x² + (2xy³ + 5xy³) - 4y² = x² + 7xy³ - 4y²

Bậc của đa thức

- Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.

Ví dụ:

A = x² + 7xy³ - 4y² => Bậc của đa thức A là 4

- Một số khác 0 tùy ý được coi là một đa thức bậc 0.

- Số 0 cũng là một đa thức, gọi là đa thức không. Nó không có bậc xác định.

Cách giải bài tập đa thức

* Dạng bài tập nhận dạng đa thức:

- Căn cứ vào khái niệm đa thức nhận dạng đa thức.

Ví dụ: Biểu thức nào sau đây là đa thức? Hãy chỉ rõ các hạng tử của mỗi đa thức ấy.

3xy² − 1; x + 2/x; –√2x + 3; 4y

Giải:

Biểu thức là đa thức: 3xy² − 1; –√2x + 3

Các hạng tử của mỗi đa thức:

Đa thức 3xy² − 1 có các hạng tử là: 3xy²; − 1

Đa thức –√2x + 3 có các hạng tử là: –√2x; 3

* Dạng bài tập thu gọn và tìm bậc của đa thức, tính giá trị của đa thức:

- Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn đa thức

- Căn cứ vào đa thức đã rút gọn và xác định bậc của đa thức: Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.

- Đối với trường hợp cho giá trị biến của đa thức, thì thay các giá trị biến đã cho vào đa thức rồi tính giá trị.

Ví dụ 1: Với mỗi đa thức sau, thu gọn (nếu cần) và tìm bậc của nó:

a) Q = 5x² − 7xy + 2,5y² + 2x − 8,3y + 1

b) H = 4x⁵ − 12x³y + 3/4x²y² − 4x⁵ + 2y² − 7

Giải:

a) Đa thức Q đã ở dạng thu gọn.

Đa thức Q = 5x² − 7xy + 2,5y² + 2x − 8,3y + 1 có bậc là 2.

b) Rút gọn đa thức H:

H = 4x⁵ − 12x³y + 3/4x²y² − 4x⁵ + 2y² − 7 = −12x³y + 3/4x²y² + 2y² −7  có bậc là 4

Ví dụ 2: Thu gọn, tìm bậc và tính giá trị của của mỗi đa thức sau với x = 1 và y = 2

a) x⁴ − 3x²y² + 3xy² − x⁴ + 1

b) 5x²y + 8xy − 2x² − 5x²y + x²

Lời giải:

a) Thu gọn đa thức:

Ta có: x⁴ − 3x²y² + 3xy² − x⁴ + 1 = (x⁴ − x⁴) − 3x²y² + 3xy² + 1 = − 3x²y² + 3xy² + 1

=> Bậc của đa thức là 4

=> Với x = 1 và y = 2 ta có: − 3.1².2² + 3.1.2² + 1 = 1

Giá trị của đa thức tại x = 1 và y = 2 là 1

b) Thu gọn đa thức:

Ta có: 5x²y + 8xy − 2x² − 5x²y + x² = (5x²y − 5x²y) + 8xy + (− 2x² + x²) = 8xy − x²

=> Bậc của đa thức là 2

=> Với x = 1 và y = 2 ta có: 8.1.2 − 1² = 15

Giá trị của đa thức tại x = 1 và y = 2 là 15

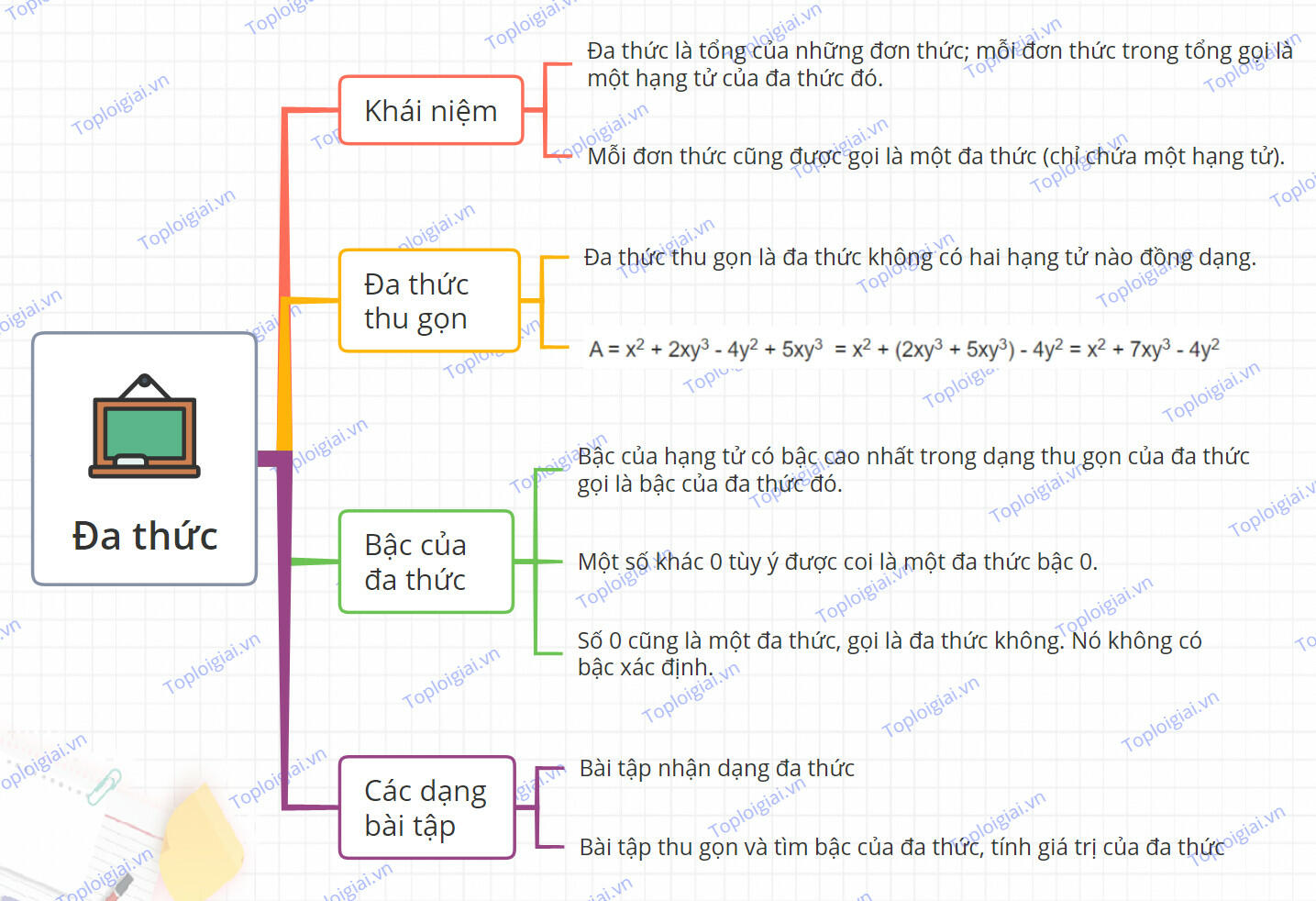
Sơ đồ tư duy Đa thức