Lập phương của một tổng. Lập phương của một hiệu

Hệ thống kiến thức về lập phương của một tổng hay một hiệu, cách giải bài tập lập phương của một tổng và lập phương của một hiệu  Toán 8 chi tiết, dễ hiểu bám sát chương trình Sách mới.

1. Lập phương là gì?

Trong số học, lập phương của một số n có nghĩa là nhân 3 lần giá trị của nó với nhau: n³ = n × n × n. Hay cũng có thể hiểu là lấy tích của nó với bình phương của nó. 

2. Cách tính lập phương một tổng

* Khái niệm: Lập phương của một tổng là một công thức toán học, được sử dụng để tính giá trị lập phương của tổng của hai số. Cụ thể, nếu ta có hai số là a và b, thì lập phương của một tổng của hai số này sẽ bằng với lập phương của số a cộng với ba lần tích bình phương của số a nhân số b, cộng thêm ba lần tích số a nhân với bình phương của số b, và cộng cuối cùng với lập phương của số b. Công thức này được phát biểu như sau: (a + b)³ = a³ + 3a²b + 3ab² + b³.

* Cách tính lập phương của một tổng

Lập phương của tổng hai số a và b = lập phương số a + 3ab(a + b) + lập phương số b

Trong đó:

- a và b là hai số cần tính lập phương của tổng

- ab là tích của a và b

Ví dụ: Tính giá trị của biểu thức:

a) A = x³ + 3x² + 3x + 2 tại x = -1

b) B = x³ + 9x² + 27x + 27 tại x = 17

Lời giải:

a) Ta có:

A = x³ + 3x² + 3x + 2

A = x³ + 3x² + 3x + 1 + 1

A = (x + 1)³ + 1

Thay x = -1 vào biểu thức ra có:

A = (-1 + 1)³ + 1

A = 0³ + 1

A = 1

Vậy A = 1

b) Ta có:

B = x³ + 9x² + 27x + 27

B = x³ + 3.x².3 + 3.x.3² + 3³

B = (x + 3)³

Thay x = 17 vào biểu thức ta có:

B = (17 + 3)³ = 20³ = 8000

Vậy B = 8000

3. Cách tính lập phương của một hiệu

- Lập phương của một hiệu bằng lập phương của biểu thức thứ nhất trừ 3 lần tích của bình phương biểu thức thứ nhất và biểu thức thứ hai cộng 3 lần tích biểu thức thứ nhất và bình phương biểu thức thứ hai rồi trừ với lập phương của biểu thức thứ hai.

- Lập phương của một hiệu là biểu thức lập phương của hiệu hai số. Để tính lập phương của một hiệu ta sử dụng hằng đẳng thức sau đây:

(a - b)³ = a³ - 3a²b + 3ab² - b³

Trong đó a và b là hai số bất kỳ.

Ví dụ: 

a) Khai triển hằng đẳng thức (2x - 3y)³

b) Viết biểu thức 8 - 12x + 6x2 - x³ dưới dạng lập phương của một tổng.

Lời giải:

a) Khai triển hằng đẳng thức (2x - 3y)³ ta được:

(2x - 3y)³

= (2x)³ - 3.(2x)²(3y) + 3(2x).(3y)² - (3y)³

= 8x³ - 36x²y + 54xy² - 27y³

b) Viết biểu thức 8 - 12x + 6x² - x³ dưới dạng lập phương của một tổng ta được:

8 - 12x + 6x² - x³

= 2³ - 3.2².x + 3.2.x² - x³

= (2 - x)³

4. Bài tập vận dụng

Câu 1. Viết các biểu thức sau đây dưới dạng lập phương của một tổng hoặc một hiệu:

a) a³ + 12a² + 48a + 64

b) 27x³ + 54x²y + 36xy²+ 8y³

c) x³ − 9x²y + 27x − 27

d) 8a³ −12a²b + 6ab² − b³

Giải:

a) a³ + 12a² + 48a + 64

= a³ + 3.a².4 + 3.a.4² + 4³

= (a+4)³

b) 27x³ + 54x²y + 36xy² + 8y³

= (3x)³ + 3.(3x)²y + 3.3x.(2y)² + (2y)³

= (3x + 2y)³

c) x³ − 9x²y + 27x−27

= x³ − 3.x².3 + 3.x.3² + 3³

= (x−3)³

d) 8a³−12a²b + 6ab² − b³

= (2a)³ − 3.(2a)²b + 3.2a.b²−b³

= (2a−b)³

Câu 2: Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến x.

D = (x+2)³ − (x−2)³ − 12(x²+1)

Giải:

D = (x+2)³−(x−2)³ − 12(x²+1)

= (x³ + 3.x².2+3.x.2²+2³)−(x³−3.x².2+3.x.2²−2³)−12x²−12

= x³ + 6x² + 12.x+2³ − x³ + 6x² − 12x + 8 −12x²−12=−4

Giá trị của biểu thức D luôn luôn bằng -4 với mọi x

Câu 3: Tính nhanh: (0,76)³ + (0,24)³ + 3.0,76.0,24

Giải:

(0,76)³ + (0,24)³ + 3.0,76.0,24

= (1 − 0,24)³ + (0,24)³ + 3.(1−0,24).0,24

= 1 − 3.1.0,24 + 3.1.0,242 − (0,24)³ + (0,24)³ + 3.0,24 − 3.(0,24)²

= 1

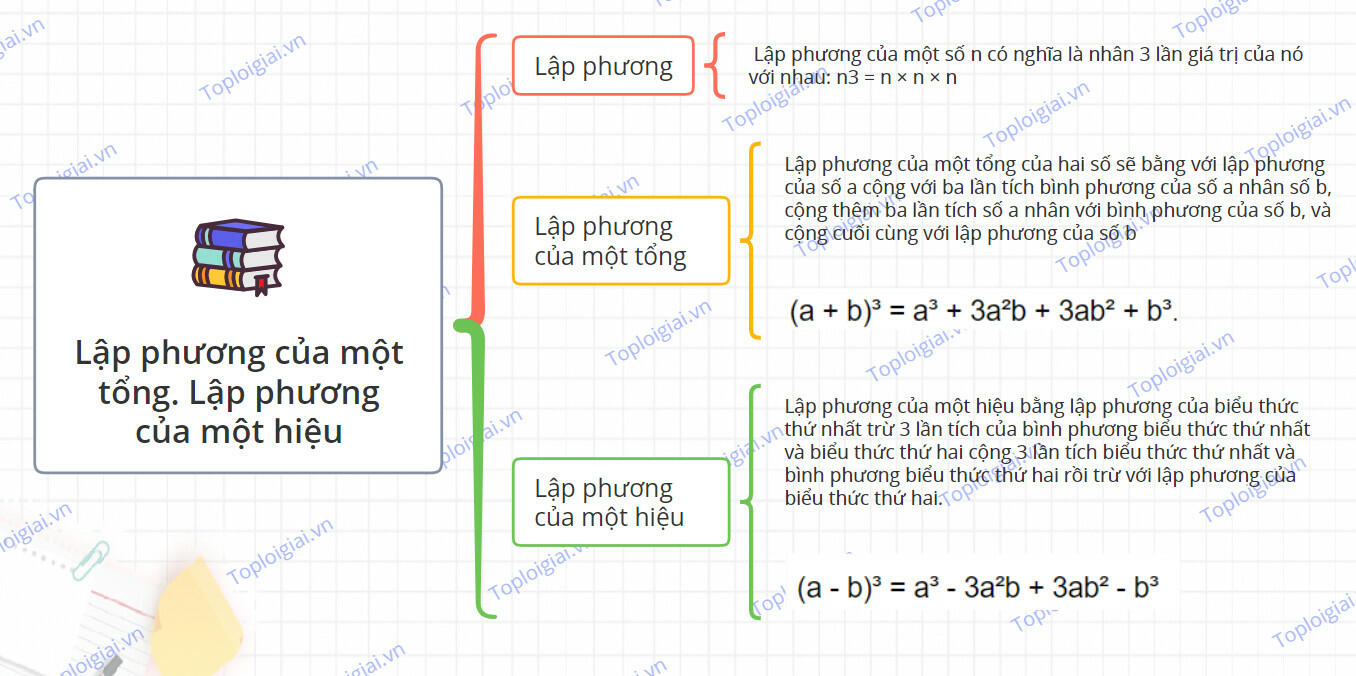
5. Sơ đồ tư duy Lập phương của một tổng. Lập phương của một hiệu