Bài 36 trang 92 sbt Toán 8 tập 2

Bài 6: Trường hợp đồng dạng thứ hai (c.g.c)

Bài 36 trang 92 sbt Toán 8 tập 2

Hình thang ABCD (AB // CD) có AB= 4cm, CD = 16cm và BD = 8cm. Chứng minh: ∠(BAD) = ∠(DBC) và BC =2AD.

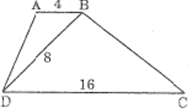
Lời giải:

Ta có: 

Suy ra: 

Xét ΔABD và ΔBDC, ta có:

∠(ABD) = ∠(BDC) (so le trong)

 (chứng minh trên)

Vây ΔABD đồng dạng ΔBDC (c.g.c) ⇒ ∠(BAD) = ∠(DBC)

Tỉ số đồng dạng k = 1/2

Ta có:   , suy ra: BC = 2AD

Xem toàn bộ Giải SBT Toán 8: Bài 6: Trường hợp đồng dạng thứ hai (c.g.c)