Bài 9: Tích của một vectơ với một số

Hướng dẫn Giải Toán 8 Kết nối tri thức Bài 9: Tích của một vectơ với một số ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 10 trang 55

Hoạt động 1: Cho vecto AB = a. Hãy xác định điểm C sao cho BC = a.

a. Tìm mối quan hệ giữa vecto AB và vecto a + vecto a

b. Vecto a + vecto a có mối quan hệ như thế nào về hướng và độ dài đối với vecto a?

Lời giải

Điểm C nằm trên tia AB sao cho BC = a. 

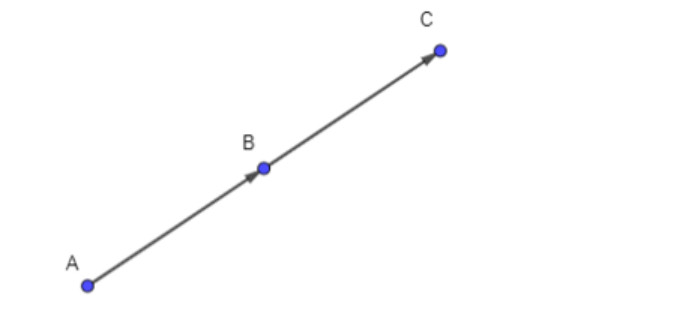
a) vecto a + vecto a= vecto AC

Vậy vecto a + vecto a cùng hướng và có độ dài gấp đôi so với vecto AB

b. Vậy vecto a + vecto a cùng hướng và có độ dài gấp đôi so với vecto a

Câu hỏi: 1a→ và a→ có bằng nhau hay không?

Lời giải

Có bằng nhau.

Giải Toán 10 trang 56

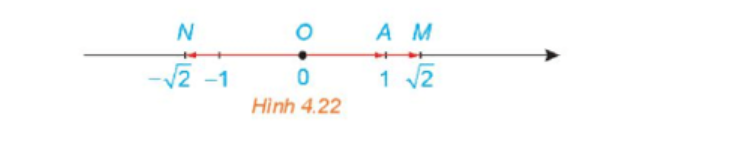
Hoạt động 2: Trên một trục số gọi O, A, M, N tương ứng biểu thị các số 0; 1;√2;-√2. Hãy nêu mối quan hệ về

hướng và độ dài của mỗi vecto OM , vecto ON với vecto a = vecto OA. Viết đẳng thức thể hiện mối quan hệ

giữa hai vecto OM, vecto OA.

Lời giải

+ Vecto OM cùng hướng với vecto OA và vecto OM = √2 vectoOA.

+ Vecto ON ngược hướng với vecto OA và vecto ON = √2 vecto OA.

Đẳng thức biểu thị mối quan hệ giữa hai vecto OM và vecto OA là vecto OM=√2 vecto OA.

Câu hỏi: vecto −a và (−1) vecto a có mối quan hệ gì?

Lời giải

Ta có: vecto −a = (−1). vecto a

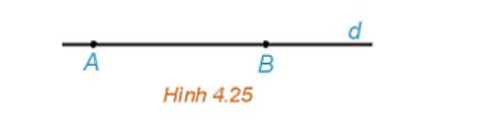
Luyện tập 1: Cho đường thẳng d đi qua hai điêm phân biệt A và B. Những khẳng định nào sau đây là đúng?

a. Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để vecto AM = vecto tAB.

b. Với điểm M bất kì, ta luôn có vecto AM = AM/AB .vecto AB

c. Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số t≤0 để vecto AM = t vecto AB.

Lời giải

- Nếu M thuộc đường thẳng d thì vecto AM cùng phương vecto AB

Do đó ta có tồn tại một số thực t thỏa mãn AM = tvectoAB.

Nếu tồn tại số t thỏa mãn vecto AM = t vectoAB thì vecto AM cùng phương AB hay AM trùng với vecto AB.

Do đó A, M, B thẳng hàng hay M thuộc đường thẳng d.

Vì thế khẳng định a) đúng.

- Khẳng định b,c sai

Giải Toán 10 trang 57

Hoạt động 3: Với vecto u ≠ vecto 0 và hai số thực k, t, những khẳng định nào sau đây đúng?

a. Hai vecto k(tvectou) và (kt)vecto u có cùng độ dài bằng |kt||vectou|.

b. Nếu kt ≥ 0 thì cả hai vecto k(tvectou), (kt)vectou cùng hướng với vecto u.

c. Nếu kt < 0 thì cả hai vecto k(tvectou), (kt)vectou ngược hướng với vectou.

d. Hai vecto k(tvectou), (kt)v ecto u bằng nhau.

Lời giải

Khẳng định đúng là: a, b, c, d.

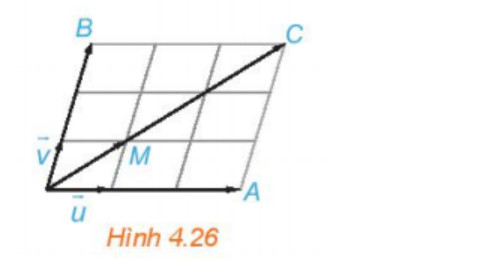
Hoạt động 4: Hãy chỉ ra trên Hình 4.26 hai vecto 3(vecto u + vecto v) và 3 vecto u+3 vecto u. Từ đó, nêu mối quan

hệ giữa 3(vecto u + vecto v và 3 vecto u+3 vecto u

Lời giải

Xét hình bình hành OEMF, ta có: 

vecto u + vecto v = vecto OE + vecto OF = vecto OM ( theo quy tắc hình bình hành)

⇒ 3(vecto u + vectov) = 3 vecto OM = vecto OC

Xét hình bình hành OACB, ta có:

3u + 3v = vecto OA + vecto OB = OC (theo quy tắc hình bình hành)

⇒ 3(vecto u + vecto v) = 3 vecto u + 3vecto v(=OC)

Vậy 3(vecto u + vecto v) = 3 vecto u + 3 vecto v.

Luyện tập 2: Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có: vecto OA + vecto OB +

vecto OC = 3vectoOG

Lời giải 

Vì G là trọng tâm tam giác ABC nên ta có: 

vecto GA + vectoGB + vecto GC = vecto0

=> vecto OA − vecto OG + vecto OB − vecto OG + vecto OC − vecto OG = vecto 0

Như vậy vecto OA + vecto OB + vecto OC = 3 vecto OG

Luyện tập 3: Trong hình 4.27, hãy biểu thị mỗi vecto u, vecto v theo hai vecto vecto a, vecto b, tức là tìm các số x,

y, z, t để vecto u=x vectoa + y vecto b, vecto v = t vecto a + zvecto b.

Lời giải

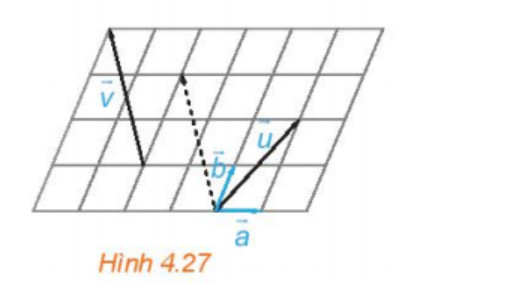
vecto u = vecto OB = vecto OA + vecto OC = 2 vecto a + 2 vecto b,
vecto v = vecto ON = vecto OM + vecto OP = 3vecto b − 2vecto a = −2vectoa + 3vectob.