Bài 3.3 trang 37 SGK Toán 10 Tập 1 Kết nối tri thức

Bài 5: Giá trị lượng giác của một góc từ 0^o đến 180^o

 Bài 3.3 trang 37 SGK Toán 10 Tập 1 Kết nối tri thức:

Chứng minh các hệ thức sau:

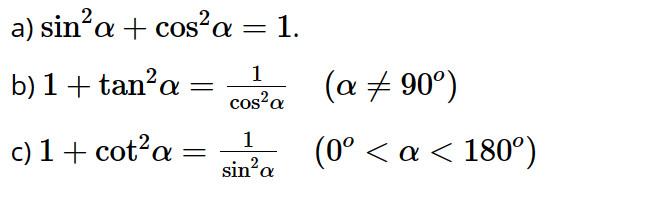
Lời giải:

a. Trên nửa đường tròn đơn vị như hình ta xét: góc xOM = α, gọi N và P lần lượt là hình chiếu của M trên Ox và Oy thì sinα = OP và cosα = ON.

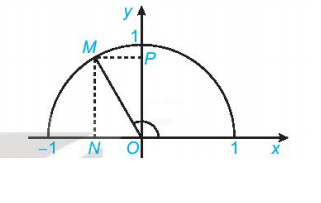
Ta chứng minh: OP²  + ON² =1

Thật vậy:

Vì ΔPMO = ΔNOM nên OP = MN.

Áp dụng định lí Pytago cho tam giác NOM ta có:

MN²  + ON² = OM²  =1.

=> OP²  + ON² =1

Vậy sin²α + cos²α = 1

b. Xét vế trái 1 + tan²α = 1 + sin²α.cos²α = sin²α + cos²α.cos²α = 1cos²α

Vậy 1 + tan²α=1cos²α (α≠90^o)

c. Xét vế trái 1+cot²α = 1+cos²α.sin²α = sin²α + cos²α.sin²α = 1sin²α

Vậy 1 + cot²α = 1sin²α(0^o<α<180^o)