Bài 10: Vectơ trong mặt phẳng tọa độ

Hướng dẫn Giải Toán 8 Kết nối tri thức Bài 10: Vectơ trong mặt phẳng tọa độ ngắn gọn kèm lời giải và đáp án chi tiết bám sát nội dung chương trình Sách mới.

Giải Toán 10 trang 60

Hoạt động 1: Trên trục số Ox, gọi A là điểm biểu diến số 1 và đặt vecto OA = vecto i (H4.32a). Gọi M là điểm biểu

diễn số 4, N là điểm biểu diễn số −32. Hãy biểu thị mỗi vecto OM = vecto ON theo vecto i. 

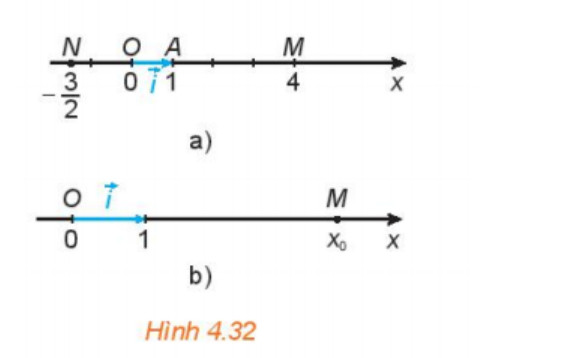
Lời giải

vecto OM cùng hướng với vecto OA và vecto OM = 4 vecto OA nên ta có:

vecto OM = 4 vecto OA = 4 vecto i.

Ta có: vecto ON ngược hướng với vecto OA và vecto ON = 3/2 vecto OA 

=> vecto ON = −3/2 vecto OA = −3/2 vecto i.

Hoạt động 2: Trong Hình 4.33:

a. Hãy biểu thị mỗi vecto OM, vecto ON theo các vecto i; vecto j.

b. Hãy biểu thị vecto MN theo các vecto OM, vecto ON, từ đó biểu thị vecto MN theo các vecto i; vecto j.

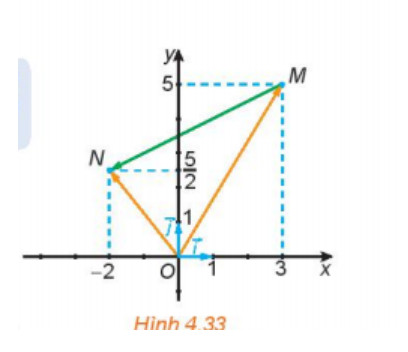
Lời giải

a. vecto OM = vecto  OH + vecto OK

= 3 vecto i + 5 vecto j. ( Quy tắc hình bình hành)

vecto ON = vecto OP + vecto OQ

= −2 vecto i + 5/2 vecto j ( Quy tắc hình bình hành)

b. vecto MN = vecto ON + vecto OM

= −2 vecto i + 5/2 vecto j - (3 vecto i + 5 vecto j)

= −5 vecto i + −5/2 vecto j

Luyện tập 1: Tìm tọa độ của vecto 0

Lời giải

vecto 0 có tọa độ là (0; 0).

Hoạt động 3: Trong mặt phẳng tọa độ Oxy, cho vecto u = (2; -3), vecto v = (4;1), vecto a = (8;-12).

a. Hãy biểu thị mỗi vecto u, vecto v, vecto a theo các vecto i, vecto j.

b. Tìm tọa độ của các vecto u + vecto v, 4 vecto u.

c. Tìm mối liên hệ giữa hai vecto u, vecto a.

Lời giải

a)

vecto u = 2 vecto i + (−3) vecto j

vecto v = 4 vecto i + 1 vecto j.

vecto a = 8 vecto i + (−12) vecto j

b)

vecto u + vecto v = 6i + (−2) vecto j nên có tọa độ là (6; -2).

4 vecto u = 8 vecto i + (−12) vecto j  nên có tọa độ là (8; -12)

c) 

4 vecto u = vecto a.

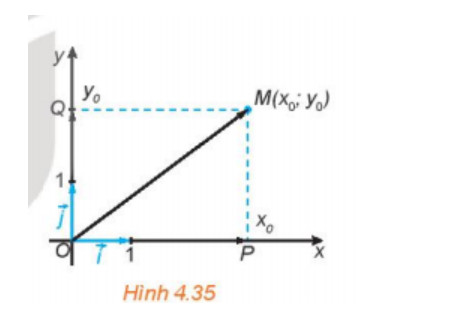
Hoạt động 4: Trong mặt phẳng tọa độ Oxy, cho điểm M(xo; yo). Gọi P, Q tương ứng là hình chiếu vuông góc của

M trên trục hoành Ox và trục tung Oy (H.4.35).

a. Trên trục Ox, điểm P biểu diễn số nào? Biểu thị vecto OP theo vecto i và tính độ dài của vecto OP theo x_o.

b. Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị vecto OQ theo vecto j và tính độ dài của vecto OQ theo y_o.

c. Dựa vào hình chữ nhật OPMQ, tính độ dài của OM theo x_o; y_o.

d. Biểu thị OM theo các vecto i, vecto j.

Lời giải

a) Trên trục Ox, điểm P biểu diễn cho số x₀;

Độ dài đoạn thẳng OP = |x₀| = x₀.

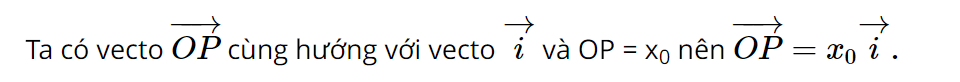
b) Trên trục Oy, điểm Q biểu diễn cho số y₀;

Độ dài đoạn thẳng OQ = |y₀| = y₀.

Hoạt động 5: Trong mặt phẳng tọa độ Oxy, cho các điểm M(x; y) và N(x'; y').

a. Tìm tọa độ của các vecto OM, vecto ON

b. Biểu thị vecto MN theo các vecto OM, ON và tìm tọa độ của vecto MN .

c. Tìm độ dài của vecto MN.

Lời giải

a. vecto OM (x;y); vecto ON (x′;y′)
b. vecto MN = vecto ON − vecto OM
=> vecto MN (x′ − x; y′ − y)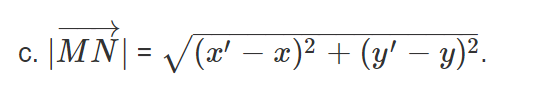

Luyện tập 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1). B(3; 3).

a. Các điểm O, A, B có thẳng hàng hay không?

b. Tìm điểm M(x; y) để OABM là một hình bình hành.

Lời giải

a. Xét vecto OA (2;1) và vecto OB (3;3) không cùng phương vì 23 ≠ 13. 

Do đó các điểm O, A, B không thẳng hàng.

b. OABM là hình bình hành khi  và chỉ khi vecto OA = vecto MB.

Ta có: vecto OA (2;1) và vecto MB (3 − x; 3 − y)

vecto OA = vecto MB ⇔ 3 − x = 2 và 3 − y = 1 ⇔ x = 1; y = 2

Vậy điểm cần tìm là M (1; 2).