Bài 17 trang 63 SGK Toán 7 tập 2

Bài 3: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác

Bài 17 (trang 63 SGK Toán 7 tập 2)

Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC.

a) So sánh MA với MI + IA, từ đó chứng minh MA + MB < IB + IA

b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB.

c) Chứng minh bất đẳng thức MA + MB < CA + CB.

Lời giải: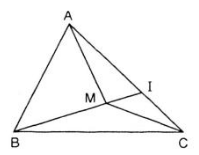

a) M nằm trong tam giác nên M không nằm trên cạnh AC.

⇒ A, M, I không thẳng hàng.

Xét bất đẳng thức tam giác trong ΔAMI:

MA < MI + IA

⇒ MA + MB < MB + MI + IA (cộng MB cả hai vế)

hay MA + MB < IB + IA (vì MB + MI = IB).

b) Ba điểm B, I, C không thẳng hàng.

Xét bất đẳng thức tam giác trong ΔIBC:

IB < IC + CB

⇒ IB + IA < IA + IC + BC (cộng với IA cả hai vế)

hay IB + IA < CA + CB (vì IA + IC = AC)

c) Theo kết quả câu a và câu b

MA + MB < IB + IA < CA + CB nên MA + MB < CA + CB.

Xem toàn bộ Giải Toán 7: Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác