Câu hỏi 4 trang 34 Toán 11 Đại số Bài 3

Bài 3: Một số phương trình lượng giác thường gặp

Câu hỏi 4 trang 34 Toán 11 Đại số Bài 3

Giải phương trình 3cos²6x + 8sin3x cos3x – 4 = 0.

Lời giải

3cos²6x + 8sin3x cos3x - 4 = 0

⇔3(1-sin²6x) + 4sin6x - 4 = 0

⇔-3sin²6x + 4sin6x - 1 = 0

Đặt sin6x = t với điều kiện -1 ≤ t ≤ 1 (*),

ta được phương trình bậc hai theo t:

-3t² + 4t - 1 = 0(1)

Δ = 4² - 4.(-1).(-3) = 4

Phương trình (1) có hai nghiệm là:

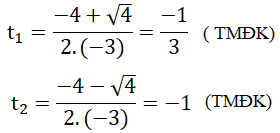
Ta có:

sin6x = (-1)/3 ⇔ 6x = arcsin(-1)/3 + k2π và 6x = π - arcsin(-1)/3 + k2π

⇔ x = 1/6 arcsin(-1)/3 + k π/3, và x = π/6 - 1/6 arcsin(-1)/3 + kπ/3, k ∈ Z

sin6x = -1 ⇔ sin6x = sin(-π)/2

⇔ 6x = (-π)/2 + k2π, k ∈ Z

⇔ x = (-π)/12 + kπ/3, k ∈ Z

Xem toàn bộ Giải Toán 11: Bài 3. Một số phương trình lượng giác thường gặp