Bài 41 trang 127 SGK Đại Số 10 nâng cao

Luyện tập (trang 127)

Bài 41 (trang 127 SGK Đại Số 10 nâng cao)

Giải và biện luận các hệ bất phương trình :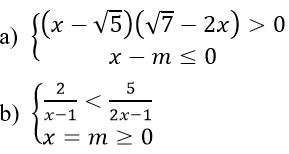

Lời giải:

a) Lập bảng xét dấu vế trái của bất phương trình (x-√5)(√7-2x)>0 ta suy ra tập nghiệm là : T₁=(√7/2; √5)

Từ đó ta suy ra:

Nếu m≤√(7 )/2 thì hệ vô nghiệm

Nếu m ∈ (√7/2; √5) thì tập nghiệm của hệ là : T=(√7/2;m]

Nếu m ≥ √5 thì tập nghiệm của hệ là : (√7/2; √5)

b) Ta có: 2/(x-1)<5/(2x-1)=>1/2<x<1 hoặc x>3

Như vậy tập nghiệm của bất phương trình đầu là:

T₁=(1/2;1)∪(3;+∞)

Dễ dàng có tập nghiệm của bất phương trình x-m≥0 là T₂=[m;+∞)

Do đó:

Nếu m ≤ 1/2 thì tập nghiệm của hệ là : T=(1/2;1)∪(3; +∞)

Nếu 1/2<m<1 thì tập nghiệm T = [m;1)∪(3;+∞)

Nếu m ≥ 1 và m ≤ 3 thì tập nghiệm T = (3;+∞)

Nếu m>3 thì tập nghiệm T=[m;+∞)

Tham khảo toàn bộ: Giải bài tập Toán 10 nâng cao