Các dạng bài tập về số hữu tỉ lớp 7 có đáp án

Tổng hợp các dạng bài tập về số hữu tỉ đầy đủ, hay nhất. Giúp các em có thể nắm vững kiến thức về số hữu tỉ. Hãy cùng thầy Phú Toploigiai khám phá và tìm hiểu những kiến thức bổ ích qua bài viết chi tiết dưới đây!

1. Các dạng bài tập về số hữu tỉ 

Dạng 1: Thực hiện các phép tính có liên quan đến số hữu tỉ

Phương pháp giải: Để giải các bài tập về thực hiện phép tính có liên quan đến số hữu tỉ, đầu tiên cần đưa các số hữu tỉ về dạng phân số, sau đó áp dụng các quy tắc tính toán với phép tính cộng, trừ, nhân, chia số hữu tỉ.

Ví dụ: Tính 

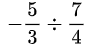
Đáp án: 

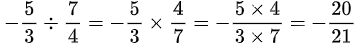
Dạng 2: Biểu diễn số hữu tỉ trên trục số

Phương pháp giải: Cần xác định số hữu tỉ là số hữu tỉ dương hay số hữu tỉ âm, sau đó tiếp tục thực hiện các bước tiếp theo:

- Nếu số hữu tỉ a/b là số hữu tỉ dương: Trên trục số, chiều dương trục, tiến hành chia độ dài 1 đơn vị thành b phần bằng nhau. Sau đó lấy điểm trên chiều dương trục Ox điểm a phần và xác định vị trí số hữu tỉ a/b.

- Nếu số hữu tỉ a/b là số hữu tỉ âm: Trên trục số, chiều âm trục, tiến hành chia độ dài 1 đơn vị thành b phần bằng nhau. Sau đó lấy điểm trên chiều âm trục Ox điểm a phần và xác định vị trí số hữu tỉ a/b.

Dạng 3: So sánh số hữu tỉ

Phương pháp giải: Đưa các số hữu tỉ đã cho về dạng phân số có cùng mẫu số dương, sau đó tiến hành so sánh tử số. Nâng cao hơn chúng ta có thể thực hiện việc so sánh với phân số trung gian để tìm ra đáp án.

Dạng 4: Xác định số hữu tỉ là âm, dương hay 0

Phương pháp giải: Giải bài tập dạng 4 học sinh cần căn cứ vào tính chất của số hữu tỉ để xác định số hữu tỉ là số âm, số dương hay là 0.

Ví dụ: Cho số hữu tỉ x = (a – 25)/29, hãy xác định giá trị của a để:

x là số âm
x là số dương
x = 0
Đáp án:

x là số âm => (a – 25)/29 < 0 => a – 25 < 0 => a < 25

x là số dương => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

x = 0 => (a – 25)/29 =0 0 => a – 25 = 0 => a = 25

Dạng 5: Tìm số hữu tỉ trong khoảng theo điều kiện cho trước

Phương pháp giải: Nếu đề bài yêu cầu tìm số hữu tỉ theo trong khoảng theo điều kiện cho trước, chúng ta cần đưa các số hữu tỉ về cùng tử số hoặc mẫu số để tìm ra đáp án.

Ví dụ: Tìm giá trị của m để m/18 lớn hơn -5/6 và nhỏ hơn -1/

Hướng dẫn đáp án

Quy đồng mẫu số các phân số như sau:

Mẫu thức chung: 18

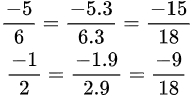
Theo đề bài ra ta có:

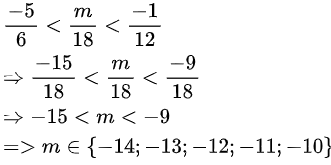
Dạng 6: Tìm x với số hữu tỉ

Phương pháp giải: Với dạng toán tìm x với số hữu tỉ cần phải thực hiện quy đồng khử mẫu số và chuyển x về 1 vế, các số hạng còn lại về 1 về. Từ đó tính giá trị của x

Ví dụ: Tìm x biết x . (2/ 3) + 5/ 6 = 1/ 8

Đáp án:

x . (2/ 3) + 5/ 6 = 1/ 8

=> x . (2/ 3) = 1/ 8 + 5/ 6

=> x = 46/ 48 : 2/ 3

=> x = 23 . 3 / 24 . 2

=> 23/16

Dạng 7: Tìm a để biểu thức là số nguyên

Phương pháp giải: Đối với bài toán tìm a nếu tử số không chứa a chúng ta cần sử dụng dấu chia hết, nếu tử số chứa a dùng dấu chia hết hoặc tách tử số theo mẫu số. Nếu bài toán yêu cầu tìm đồng thời cả a, b cần nhóm a hoặc b và đưa về dạng phân thức để tính.

Ví dụ: Tìm số nguyên a với điều kiện 8/(a – 1) là số nguyên

Đáp án:

Điều kiện: a – 1 ≠ 0 => a ≠ 1

Để a là số nguyên => 8 chia hết cho (a – 1)

=> (a – 1) là ước của 8 => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (a – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> a = {-7, -3, -1, 0, 3, 5, 9}

2. Bài tập vận dụng về số hữu tỉ

Bài 1: 

Lời giải:

Ta có: 

Chọn đáp án A

Bài 2: 

A. Là số nguyên âm

B. Là số nguyên dương

C. Là số hữu tỉ âm.

D. Là số hữu tỉ dương.

Lời giải:

Ta có: 

Là số hữu tỉ âm

Chọn đáp án C.

Bài 3: Số -3/14 là hiệu của hai số hữu tỉ nào dưới đây?

Lời giải

Ta có:

Chọn đáp án C.

Bài 4: Tính giá trị các biểu thức sau:

 B = −1/10−1/100−1/1000−1/10000−1/100000−1/1000000.

Lời giải:

 B = −1/10−1/100−1/1000−1/10000−1/100000−1/1000000

= −(0,1+0,01+0,001+0,0001+0,00001+0,000001) = −0,111111.

Bài 5: Tính:

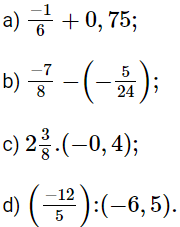
Lời giải: