Một số dạng bài tập toán về hình tứ giác

Một số dạng bài tập toán về hình tứ giác bài viết này sẽ hướng dẫn các em các phương pháp giải các bài tập hiệu quả để đầy đủ, hay nhất. Hãy cùng thầy Phú toploigiai khám phá và tìm hiểu những kiến thức bổ ích qua bài viết chi tiết dưới đây!

Các dạng bài tập

Dạng 1. Tính số đo góc

Dựa vào tính chất tổng các góc trong một tứ giác.

Ví dụ:

Lời giải:

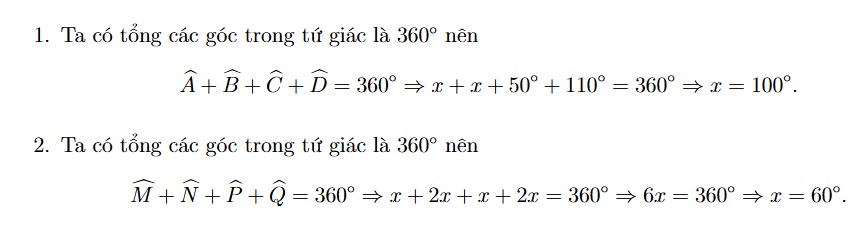
Dạng 2. Dạng toán chứng minh hình học

Vận dụng các kiến thức đã được học như bất đẳng thức tam giác, chu vi, đường trung trực của đoạn thẳng,..

Ví dụ:

Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. Chứng minh:

1. AC + BD > AB + CD;

2. AC + BD > AD + BC.

Lời giải:

Bài Tập Về Tứ Giác Trong Sách Giáo Khoa Lớp 8

Toán 8 Tập 1 Bài 1 trang 64: Trong các tứ giác ở hình 1, tứ giác nào luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác ?

Lời giải

a) tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác

b) tứ giác nằm trên hai nửa mặt phẳng có bờ BC (hoặc bờ CD)

c) tứ giác nằm trên hai nửa mặt phẳng có bờ AD (hoặc bờ BC)

 Toán 8 Tập 1 Bài 1 trang 65:

a) Nhắc lại định lý về tổng ba góc của một tam giác

b) Vẽ tứ giác ABCD tùy ý. Dựa vào định lý về tổng ba góc của một tam giác, hãy tính tổng A + B + C + D

Lời giải

a) Trong một tam giác, tổng ba góc là 180^o

b)

ΔABC có ∠A₁ + ∠B + ∠C₁ = 180^o

ΔADC có ∠A₂ + ∠D + ∠C₂ = 180^o

⇒∠A₁ + ∠B + ∠C₁ + ∠A₂ + ∠D + ∠C₂ = 180^o + 180^o

⇒ (∠A1 + ∠A₂ ) + ∠B + (∠C₁ + ∠C₂) + ∠D = 360^o

⇒∠A + ∠B + ∠C + ∠D = 360^o

Bài 1 (trang 66 SGK Toán 8 Tập 1): Tìm x ở hình 5, hình 6:

Lời giải:

Ta có định lý: Tổng bốn góc trong một tứ giác bằng 360º.

+ Hình 5a: Áp dụng định lý trong tứ giác ABCD ta có:

x + 110º + 120º + 80º = 360º

⇒ x = 360º – 110º – 120º – 80º = 50º

+ Hình 5b: Dựa vào hình vẽ ta có: 

Áp dụng định lý trong tứ giác EFGH ta có:

x + 90º + 90º + 90º = 360º

⇒ x = 360º – 90º – 90º – 90º = 90º.

+ Hình 5c: Dựa vào hình vẽ ta có:

Áp dụng định lý trong tứ giác ABDE ta có:

x + 90º + 65º + 90º = 360º

⇒ x = 360º – 90º – 65º – 90º = 115º

+ Hình 5d:

Áp dụng định lý trong tứ giác IKMN ta có:

x + 90º + 120º + 75º = 360º

⇒ x = 360º – 90º – 120º – 75º = 75º

+ Hình 6a: Áp dụng định lý trong tứ giác PQRS ta có:

x + x + 65º + 95º = 360º

⇒ 2x + 160º = 360º

⇒ 2x = 200º

⇒ x = 100º

+ Hình 6b: Áp dụng định lý trong tứ giác MNPQ ta có:

x + 2x + 3x + 4x = 360º

⇒ 10x = 360º

⇒ x = 36º.

Bài 2 (trang 66 SGK Toán 8 Tập 1): Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.

a) Tính các góc ngoài của tứ giác ở hình 7a.

b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):

c) Có nhận xét gì về tổng các góc ngoài của tứ giác?

Bài 3 (trang 67 SGK Toán 8 Tập 1): Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều".

a) Chứng minh rằng AC là đường trung trực của BD.

b) Tính B̂,D̂ biết rằng  = 100º, Ĉ = 60º

Lời giải:

a) Ta có:

AB = AD (gt) ⇒ A thuộc đường trung trực của BD

CB = CD (gt) ⇒ C thuộc đường trung trực của BD

Vậy AC là đường trung trực của BD

b) Xét ΔABC và ΔADC có:

   AB = AD (gt)

   BC = DC (gt)

   AC cạnh chung

⇒ ΔABC = ΔADC (c.c.c)

Bài 4 (trang 67 SGK Toán 8 Tập 1): Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở.

Lời giải:

- Cách vẽ hình 9:

+ Vẽ đoạn thẳng AB = 3cm

+ Quay cung tròn tâm A, bán kính 3cm, cung tròn tâm B bán kính 3,5cm. Hai cung tròn này cắt nhau tại C.

+ Quay cung tròn tâm C bán kính 2cm và cung tròn tâm A bán kính 1,5cm. Hai cung tròn này cắt nhau tại D.

+ Nối các đoạn BC, AC, CD, AD ta được hình cần vẽ.

- Cách vẽ hình 10:

+ Vẽ góc 

 . Trên tia Nx, lấy điểm M sao cho MN = 4cm, trên tia Ny lấy điểm P sao cho NP = 2cm.

+ Vẽ cung tròn tâm P bán kính 1,5cm và cung tròn tâm M bán kính 3cm. Hai cung tròn này cắt nhau tại Q.

+ Nối PQ, MQ ta được hình cần vẽ.

Tham khảo thêm: Định nghĩa, tính chất và dấu hiệu nhận biết của hình tứ giác