Bài 8 trang 121 Toán lớp 11 Cánh diều

Bài 8 trang 121 Toán lớp 11 Cánh diều: Cho hình lăng trụ tam giác ABC.A'B'C'. Lấy M, M' lần lượt là trung điểm các đoạn thẳng BC, B'C'; lấy các điểm G, G', K lần lượt thuộc các đoạn AM, A'M', A'B sao cho 

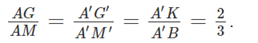
a) Chứng minh rằng C'M // (A'BM').

b) Chứng minh rằng G'K // (BCC'B').

c) Chứng minh rằng (GG'K) // (BCC'B').

d) Gọi (α) là mặt phẳng đi qua K và song song với mặt phẳng (ABC). Mặt phẳng (α) cắt cạnh CC' tại điểm I. Tính ICIC′.

Lời giải:

a) Ta có: MBM'C' là hình bình hành nên C'M // BM'

Mà BM' thuộc (A'BM')

Suy ra: C'M // (A'BM')

b)  b) △A'BM' có: A′K/A′B=A′G′/A′M′=2/3

Nên G'K // BM' mà BM' thuộc (BCC'B')

Suy ra: G'K // (BCC'B')

c) Hình bình hành AMM'A' có: GG' // MM'

Mà MM' thuộc (BCC'B')

Suy ra: GG' // (BCC'B')

Mà G'K // (BCC'B')

Do đó: (GG'K) // (BCC'B')

d) Từ K kẻ đường thẳng d cắt AA' tại E, cắt BB' tại F

Do (α) // (ABC)

Nên từ E kẻ đường thẳng // AC

Từ F kẻ đường thẳng // BC

Do đó: hai đường thẳng này cắt nhau tại I

Hình bình hành ACC'A' có: EI // AC // A'C'

Suy ra: IC/IC′=AEAE′ (1)

△A'BA có: EK // AB

Suy ra: A′K/A′B=A′E/AA′=2/3 nên AE/A′E=1/2 (2)

(1)(2) suy ra: IC/IC′=1/2